Nos Exercícios 85-90, utilize um sistema algébrico computacional para realizar as etapas a seguir:
a. Trace a função próxima ao ponto que está sendo aproximado.
b. A partir do traçado, estime o valor do limite.
86.
Passo 1
a.
A gente precisa de algum software para desenhar esse gráfico, eu vou usar o GeoGebra, mas da para fazer com qualquer um.
Escrevendo a função e dando um zoom próximo a vamos ter esse gráfico:
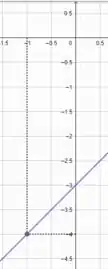
Passo 2
b.
Eu fiz a linha pontilhada para olharmos melhor aqui, quando tende a a função ta tendendo a e podemos aproximar bastante que continua tendendo sempre a . Portanto podemos estimar que
Resposta
a.
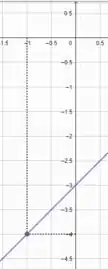
b.