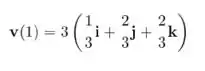Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.1 - Ex. 9
Nos Exercícios 9-14, r(t) é a posição de uma partícula no espaço no instante t. Encontre os vetores velocidade e aceleração da partícula. Em seguida, encontre o módulo da velocidade e a direção do movimento da partícula no valor determinado de t. Escreva a velocidade da partícula naquele instante como o produto de sua velocidade e versor.
Passo 1
Fala galerinha tranquilidade, seguinte nesse problema começaremos cálculando velocidade e aceleração vetorial, conforme fizemos nos exercícios anteriores, velocidade é derivada da posição em relação ao tempo e aceleração é a derivada segunda da posição em relação ao tempo ou derivada da velocidade ficando:
Velocidade:
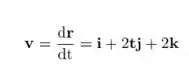
Aceleração:
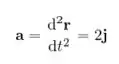
Passo 2
Nesse passo aqui precisamos do módulo da velocidade, isso pode ser feito calculando o seguinte:
A raiz quadrada das componentes ao quadrado. Ficando assim:
Passo 3
Para a direção temos podemos calcular o vetor unitário, que seria o vetor dividido pelo seu módulo, que já calculamos:
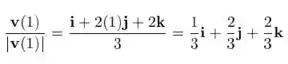
Resposta
E finalmente o produto da velocidade e seu versor:
