Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 08d
Dois carros se movem segundo os seguintes vetores posição:
d ) Em que ponto a velocidade escalar do segunda carro é mínima e qual é esta velocidade?
Passo 1
Vamos começar desparametrizando a função.
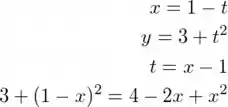
Com isso, chegamos na seguinte função do espaço sem parametrização.
Sua derivada corresponde à função da velocidade:
Como é uma reta com coeficiente angular positivo, conclui-se que quanto maior o t, maior será a velocidade. Por isso, a velocidade mínima ocorre em t = 0, que é o mínimo valor possível. Logo, o ponto é
e a velocidade vetorial é
logo, seu módulo é 1.
Resposta
O ponto é (1,3) e a velocidade é 1.
Exercícios de Livros Relacionados
Nos exercícios de 1 a 6 , σ t denota o vetor posição de uma partícula se movendo, em cada instante t . Em cada caso, determine:2)σ t = cos 2 t , - 3 sen t , t 1 = π a) o vetor velocidade V t ;
Nos exercícios de 1 a 6 , σ t denota o vetor posição de uma partícula se movendo, em cada instante t . Em cada caso, determine:3)σ t = e 2 t , t 2 , t 1 = 0 d) dois vetores tangentes unitários à traje
Nos exercícios de 1 a 6 , σ t denota o vetor posição de uma partícula se movendo, em cada instante t . Em cada caso, determine:1)σ t = 2 + cos 6 t , 2 + sen 6 t , t 1 = π 9 d) dois vetores tangent
O vetor velocidade v(t).
A velocidade escalar em t=t 1 .