Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.1 - Ex. 4

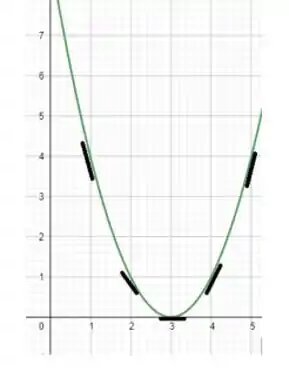
Nos exercícios de 1 a 6, ache a inclinação da reta tangente ao gráfico no ponto ( x 1 , y 1 ) . Faça uma tabela de valores de x, y e m no intervalo fechado [ a , b ] e inclua na tabela os pontos onde o gráfico tem uma tangente horizontal. Faça um esboço do gráfico e mostre um segmento da reta tangente em cada ponto colocado no gráfico.

4)   y = x 2 - 6 x + 9 ; a , b = [ 1,5 ]

Passo 1

Primeiramente iremos calcular a inclinação da reta tangente. Para isso utilizamos a seguinte definição:

m x 1 = lim ∆ x → 0 ⁡ f x 1 + ∆ x - f ( x 1 ) ∆ x

Assumindo que f x = x 2 - 6 x + 9 , temos:

f x 1 + ∆ x = x 1 + ∆ x 2 - 6 x 1 + ∆ x + 9 e

f x 1 = x 1 2 - 6 x 1 + 9

Logo, aplicando na definição:

m x 1 = lim ∆ x → 0 ⁡ = x 1 + ∆ x 2 - 6 x 1 + ∆ x + 9       - x 1 2 - 6 x 1 + 9 ∆ x

Desenvolvendo o produto notável teremos:

m x 1 = lim ∆ x → 0 ⁡ 2 x 1 ∆ x - 6 ∆ x + ∆ x 2 ∆ x

Simplificando:

m x 1 = 2 x 1 - 6

Passo 2

Agora apresentaremos uma tabela com alguns valores de x, y e m no intervalo [ 1,5 ]

Passo 3

Agora faremos o esboço do gráfico, destacando retas tangentes nos pontos escolhidos.

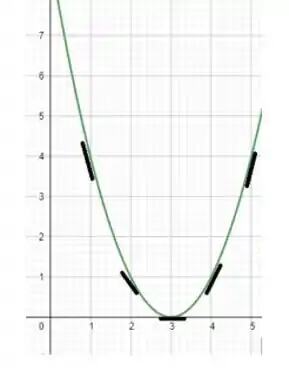
Resposta

Inclinação da reta tangente: m x 1 = 2 x 1 - 6

Tabela de valores de x, y e m:

Gráfico:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache as equações das retas tangente e normal à curva 2 x 3 + 2 y 3 - 9 x y = 0 no ponto 2 ,1 .
Prove que as retas tangentes às curvas 4 y 3 - x 2 y - x + 5 y = 0 e x 4 - 4 y 3 + 5 x + y = 0 na origem são perpendiculares.
Ache uma equação da reta tangente à curva y = x 2 + 9 , no ponto ( 4 ,5 ) .
Ache uma equação da reta normal à curva y = x 16 + x 2 na origem.
Ache uma equação da reta tangente à curva y = 7 x - 6 - 1 / 3 que seja perpendicular à reta 12 x - 7 y + 2 = 0 .