Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 23
Nos Exercícios 21-26, encontre uma parametrização para a curva
23. a metade inferior da parábola .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
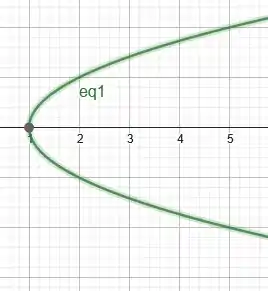
No início da tarefa, vamos desenhar uma parábola
no sistema de coordenadas cartesianas.
Como na parábola (1), x depende da variável y, então a parábola será direcionada ao longo do eixo x. Para desenhar a parábola (1), vemos pela equação que o vértice estará localizado em (por causa de em ). Com isso obtemos o gráfico da parábola:
Passo 2
Pelas condições da tarefa, sabemos que precisamos apenas da equação paramétrica da parábola localizada abaixo do eixo (a metade inferior da parábola). Quando a parábola está abaixo do eixo , então assume valores negativos. Portanto,
Escrevemos a equação da metade inferior da parábola (1) como:
Como depende de , podemos declarar com o parâmetro , ou seja,
assume valores menores ou iguais a , e então também assume valores menores ou iguais a :
Então, na equação (2), incluímos em vez de :
Nossa parametrização fica do seguinte tipo