Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.3 - Ex. 1
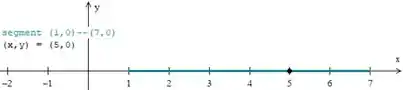
Nos exercícios 1-6, esboce o intervalo no eixo com o ponto dentro. Em seguida determine um valor de de modo que para todo ,
Passo 1
O que ele está querendo é determinar um valor de tal que a distância dos demais valores de até esteja sempre dentro do intervalo .
Para isso temos que ver qual a menor distância entre e ou entre e . Esse será o nosso valor de .
Por fim vamos esboçar o gráfico
Passo 2
A distância entre e é escrita como e vale
A distância entre e é escrita como e vale
O menor valor é a distância de a . Logo,
Passo 3
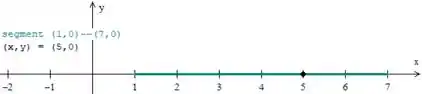
Resposta
Exercícios de Livros Relacionados
Suponha que lim x → 0 f ( x ) = 1 e lim x → 0 g ( x ) = - 5 . Especifique quais regras do teorema 1 são utilizadas para efetuar as etapas a , b , c do cálculo a seguir lim x → 0 2 f x - g x f x
Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma lim h → 0 f x + h - f ( x ) h Ocorrem com frequência em cálculo. Nos exercícios 57-62, avalie esse limite p
Suponha que lim x → 4 f ( x ) = 0 e lim x → 4 g ( x ) = - 3 . Determine lim x → 4 g x + 3 lim x → 4 x f x lim x → 4 g x 2 lim x → 4 g x f x - 1
Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma lim h → 0 f x + h - f ( x ) h Ocorrem com frequência em cálculo. Nos exercícios 57-62, avalie esse limite p
Suponha que lim x → c f ( x ) = 5 e lim x → c g ( x ) = - 2 . Determine lim x → c f x g x lim x → c 2 f x g ( x ) lim x → c f x + 3 g x lim x → c f x f x - g x