Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.Exercícios práticos - Ex. 46

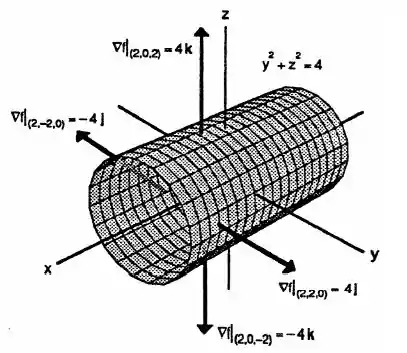
Nos Exercícios 45 e 46, esboce a superfície ƒ(x, y, z) = c juntamente com §ƒ nos pontos dados.

y 2 + z 2 = 4

( 0 ,   ± 2 ,   0 )

( 2 , 0 , ± 2 )

Passo 1

Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Para as equações paramétricas, vamos precisar do gradiente da nossa função. Ele é dado por:

∇ f = δ f δ x i + δ f δ y j + δ f δ z j

Dessa forma, para a nossa função, temos:

∇ f = 2 y j + 2 z k

Aplicado aos pontos:

( 0 ,   ± 2 ,   0 )

( 2,0 , ± 2 )

Temos:

∇ f 2 , 2 , 0 = 4 j

∇ f 2 , - 2 , 0 = - 4 j

∇ f 2 , 0 , 2 = 4 k

∇ f 2 , 0 , - 2 = - 4 k

Passo 2

Show, agora esboçando a curva com as linhas paramétricas, temos:

Resposta

∇ f 2,2 , 0 = 4 j

∇ f 2 , - 2,0 = - 4 j

∇ f 2,0 , 2 = 4 k

∇ f 2,0 , - 2 = - 4 k

Exercícios de Livros Relacionados

Determinar uma equação vetorial para a reta normal à superfície dada, nos pontos indicados: x 2 4 + y 2 + z 2 9 = 1 ; P 0 0 , 1 2 , 3 3 2
Nos Exercícios 47 e 48, encontre uma equação para o plano tangente à superfície de nível ƒ(x, y, z) = c no ponto P0. Encontre também equações paramétricas para a reta que é normal à superfície em P0.
Nos Exercícios 47 e 48, encontre uma equação para o plano tangente à superfície de nível ƒ(x, y, z) = c no ponto P0. Encontre também equações paramétricas para a reta que é normal à superfície em P0.