Nos Exercícios 31 -34, forneça a função da posição de um objeto que se desloca ao longo de um eixo em função do tempo t. Esboce, em um único gráfico, f e as funções velocidade e aceleração . Comente o comportamento do objeto em relação aos sinais e valores de v e a, incluindo os seguintes tópicos:
a. Em que instante o objeto está momentaneamente em repouso?
b. Em que instante ele se move para a esquerda (para baixo) ou para a direita (para cima)?
c. Em que instante ele muda de sentido?
d. Em que instante acelera ou desacelera?
e. Em que instante se desloca mais rapidamente (módulo da velocidade mais alto)? E de maneira mais lenta?
f. Em que instante está mais afastado da origem do eixo?
31. , (objeto pesado lançado verticalmente a partir da superfície da Terra com velocidade de 200 pés/s)
Passo 1
Inicialmente vamos achar as funções e :
e
Passo 2
Desenhando as funções , e vamos ter:
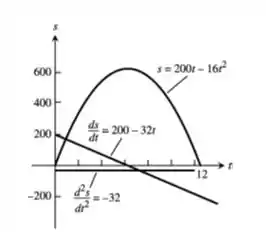
Passo 3
a.
O objeto estará momentaneamente em repouso quando sua velocidade for igual a zero. Podemos usar a função da velocidade para descobrir isso:
Passo 4
b.
Enquanto sua velocidade for positiva o corpo se move para cima, a partir do momento que a volocidade fica negativa ele troca de sentido e começa a se mover para baixo. Portanto como podemos observar no gráfico do instante zero até o instante o instante , sua velocidade é positiva e a partir disso sua velocidade fica negativa.
Passo 5
c.
Como dito na letra b, o objeto troca de sentido no instante
Passo 6
d.
Sua aceleração se mantém constante em , ou seja:
O objeto desacelera de , pois o corpo está subindo e perdendo velocidade.
E está acelerando de , pois o corpo começa a cair e ganhar velocidade.
Passo 7
e.
Podemos observar no gráfico que a velocidade é máxima no instante
E como calculado na letra a, o instante em que ele está momentaneamente em repouso é
Passo 8
f.
O instante em que o objeto está mais afstado da origem é quando ele atinge sua altura máxima. Nesse momento sua velocidade é e como calculado na letra a:
Resposta
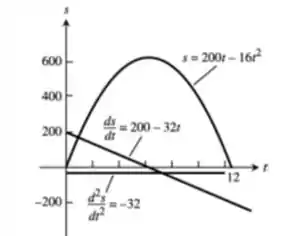
a.
b. Para cima: ; Para baixo:
c.
d. Desacelera de ; Acelera de
e. Máxima: ; Mínima:
f.