Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.4 - Ex. 27

27. Esvaziamento de um tanque Depois de aberta a válvula na parte inferior de um tanque de annazenamento, são necessárias 12 horas até que ele seja esvaziado. A profundidade y do líquido no tanque, t horas depois de a válvula ter sido aberta, é dada por

y = 6 1 - t 12 2   m

a. Determine a taxa d y / d t (m/h) do esvaziamento do tanque no instante t .

b. Quando o nível de líquido no tanque diminuirá mais rapidamente? E mais lentamente? Quais são os valores de d y / d t nesses instantes?

c. Faça um único gráfico para y e d y / d t e discuta o comportamento de y em relação aos sinais e aos valores de d y / d t .

Passo 1

a.

Só precisamos derivar a função:

d y d t = d d t 6 1 - t 12 2

d y d t = 6 d d t 1 - t 6 + t 2 144

d y d t = 6 - 1 6 + t 72

d y d t = t 12 - 1

Passo 2

b.

Observe que quanto menor o valor dessa taxa, maior é o esvaziamento, porque o sinal negativo significa o quanto de água está saindo.

Então o nível de líquido no tanque diminuir mais rapidamente, significa uma taxa de esvaziamento menor. Então quando

d y d t = t 12 - 1

for mínimo, teremos o nível de líquido do tanque diminuindo mais rapidamente.

Para essa função ser mínima t = 0 h , nesse caso:

d y d t = 0 12 - 1

d y d t = - 1 m / h

Isso quer dizer que o nível da água diminui 1 metro a cada hora.

Podemos observar que quanto mais o tempo passa, maior fica essa taxa, até que ela chegue em 0 quando t = 12 h :

d y d t = 12 12 - 1

d y d t = 0

Passo 3

c.

Quando desenhamos o gráfico ele fica assim:

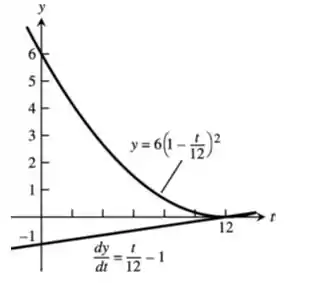
Podemos observar que enquanto t < 12 a função

y = 6 1 - t 12 2  

decresce, isso quer dizer que a derivada dela aquele ponto é negativa. E é exatamente isso que observamos na curva d y d t = t 12 - 1

Antes que ela chegue em t = 12 ela possui valores negativos.

Outra coisa que também podemos observar, é que quando a função

y = 6 1 - t 12 2

atinge seu valor mínimo em t = 12 , ela irá ter uma derivada igual a zero, o que também podemos observar na curva d y d t = t 12 - 1

para t = 12 → d y d t = 0

Resposta

a. d y d t = t 12 - 1

b. Mais rapidamente: t = 0 → d y d t = - 1   m / h

Mais lentamente: t = 12 → d y d t = 0   m / h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A equação abaixo da a posição s = f ( t ) de um corpo que se desloca em uma reta coordenada (s em metros, t em segundos). Determine a velocidade, o módulo da velocidade, a aceleração e a sobreaceleraç
23. A lei de Boyle para a expansão de um gás é P V = C , onde P é a pressão em quilogramas força por unidade de área, V é o número de unidades de volume do gás e C é uma constante. Mostre que V decres
21. Se A xc m 2 for a área de um quadrado e s cm for o comprimento de cada lado, ache a taxa de variação de A x em relação a x, quando x varia de (a) 4,000 a 4,600; (b) 4,000 a 4,300; (c) 4,000 a 4,10
Um objeto move-se ao longo de uma reta, de acordo com a equação de movimento s = 5 + t 2 , com t ≥ 0 . Ache o valor de t para o qual a medida da velocidade instantânea é (a) 0 ; (b) 1 .
Um objeto move-se ao longo de uma reta, de acordo com a equação de movimento s = 4 t 2 + 3 , com t ≥ 0 . Ache o valor de t para o qual a medida da velocidade instantânea é (a) 0 ; (b) 1 ; (c) 2 .