Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.4 - Ex. 34

Nos Exercícios 31 -34, forneça a função da posição s = f ( t ) de um objeto que se desloca ao longo de um eixo s em função do tempo t. Esboce, em um único gráfico, f e as funções velocidade v ( t ) = d s / d t = f ' ( t ) e aceleração a t = d 2 s / d t 2 = f " ( t ) . Comente o comportamento do objeto em relação aos sinais e valores de v e a, incluindo os seguintes tópicos:

a. Em que instante o objeto está momentaneamente em repouso?

b. Em que instante ele se move para a esquerda (para baixo) ou para a direita (para cima)?

c. Em que instante ele muda de sentido?

d. Em que instante acelera ou desacelera?

e. Em que instante se desloca mais rapidamente (módulo da velocidade mais alto)? E de maneira mais lenta?

f. Em que instante está mais afastado da origem do eixo?

34. s = 4 - 7 t + 6 t 2 - t 3 ,     0 < t < 4

Passo 1

Inicialmente vamos achar as funções v ( t ) e a t :

v ( t ) = d s / d t = f ' ( t )

v t = - 7 + 12 t - 3 t 2       m / s

e

a t = d 2 s / d t 2 = f " ( t )

a t = d ( d s / d t ) / d t = f " ( t )

a t = d d t ( - 7 + 12 t - 3 t 2 )

a t = - 6 t + 12       m / s 2

Passo 2

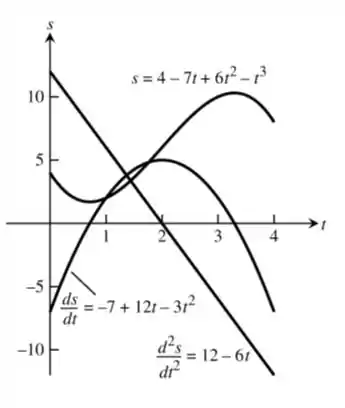
Desenhando as funções s ( t ) , v ( t ) e a t vamos ter:

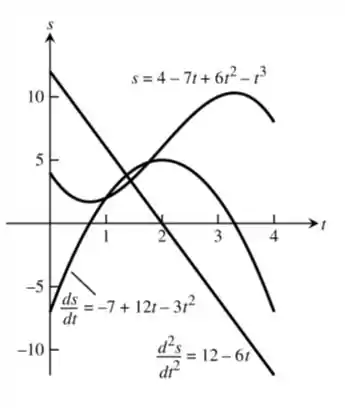
Passo 3

a.

O objeto estará momentaneamente em repouso quando sua velocidade for igual a zero. Podemos usar a função da velocidade para descobrir isso:

0 = - 3 t 2 + 12 t - 7

0 = 3 t 2 - 12 t + 7

Usando a fórmula para resolver as equações de 2°:

t = - ( - 12 ) ± - 12 2 - 4 3 7 2 ( 3 )

t = 12 ± 60 6

t = 12 ± 4 ( 15 ) 6

t = 12 ± 2 15 6

t = 6 ± 15 3   s

Passo 4

b.

Enquanto sua velocidade for negativa o corpo se move para a esquerda e quando sua volocidade é positiva, ele se move para a direita.

Portanto como podemos observar no gráfico, do instante zero até o instante o instante t = 6 - 15 3   s , sua velocidade é negativa, a partir disso sua velocidade fica positiva até o instante t = 6 + 15 3   s , quando volta a se tornar negativa novamente.

Sabemos que são nos instantes t = 6 ± 15 3   s , pois calculamos na letra a que são nesses momentos que a velocidade fica igual a zero.

Passo 5

c.

Como dito na letra b, o objeto troca de sentido nos instantes t = 6 ± 15 3   s

Passo 6

d.

A função aceleração possui um zero:

a t = - 6 t + 12

0 = - 6 t + 12

6 t = 12

t = 2   s

Portanto antes de t = 2   s sua aceleração era positiva e após esse instante ela passou a ser negativa.

No inicio o objeto está com velocidade negativa, porém sua sua aceleração é positiva logo o objeto está desacelerando, isso ocorre até o instante t = 6 - 15 3   s .

Após t = 6 - 15 3   s sua aceleração continua positiva e sua velocidade se torna positiva, ou seja, a aceleração positiva faz com que a velocidade fique cada vez maior. Portanto o corpo está acelerando até t = 2   s , onde a = 0   m / s 2 .

Após t = 2   s a aceleração fica negativa, porém sua velocidade ainda está positiva. Dessa forma o corpo vai desacelerar até o instante t = 6 + 15 3   s .

A partir desse instante o corpo acelera, pois a aceleração e a velocidade são negativas.

Passo 7

e.

Podemos observar no gráfico que a velocidade é máxima nos instantes t = 0   s e t = 4   s

E como calculado na letra a, os instantes em que ele está momentaneamente em repouso são t = 6 ± 15 3   s

Passo 8

f.

Observando o gráfico, verificamos que o instante em que o objeto está mais afastado da origem é no instante t = 6 + 15 3   s .

Resposta

v t = - 3 t 2 + 12 t - 7       m / s

a t = - 6 t + 12       m / s 2

a. t = 6 ± 15 3   s

b. Para esquerda: 0   s ≤ t ≤ 6 - 15 3   s e 6 + 15 3   s ≤ t ≤ 4   s ; Para direita: 6 - 15 3   s ≤ t ≤ 6 + 15 3   s

c. t = 6 ± 15 3   s

d. Desacelera de 0   s ≤ t < 6 - 15 3   s e de 2   s < t < 6 + 15 3   s ; Acelera de 6 - 15 3   s < t < 2   s e de 6 + 15 3   s < t ≤ 4   s .

e. Máxima: t = 0   s t = 4   s e ; Mínima: t = 6 ± 15 3   s

f. t = 6 + 15 3   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18. A figura a seguir mostra a velocidade v = f(t) de uma partícula que se movimenta ao longo de uma reta coordenada horizontal.a. Quando a partícula se move para a frente? E para trás? Quando acelera
21. Os gráficos na figura a seguir mostram a posição s, a velocidade v=d s / d t e a aceleração a = d 2 s d t 2 de um corpo que se desloca ao longo de uma reta coordenada em função do tempo t. A qual
22. Os gráficos na figura a seguir mostram a posição s , a velocidade v=d s / d t e a aceleração a = d 2 s / d t 2 de um corpo que se desloca ao longo de uma reta coordenada como funções do tempo t .
19. Queda de duas bolas A ilustração de múltiplas exposições a seguir mostra duas bolas que caem a pa1iir do repouso. As escalas verticais estão marcadas em centímetros. Use a equação s = 490 t 2 (equ
Cálculo de g em um pequeno planeta sem ar Na superfície de um pequeno planeta sem ar, exploradores usaram um estilingue para atirar uma esfera metálica verticalmente para cima com uma velocidade de la