22. Os gráficos na figura a seguir mostram a posição , a velocidade e a aceleração de um corpo que se desloca ao longo de uma reta coordenada como funções do tempo . A qual gráfico corresponde cada função? Justifique suas respostas.

Para descobrirmos qual curva é a derivada da outra, podemos olhar para os ponto em que a derivada é igual a zero e ver qual é a função, que possui valor zero, naquela coordenada . Vamos olhar para a imagem:

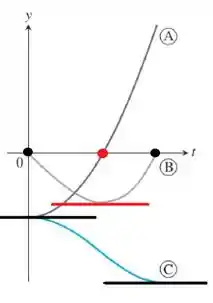
A curva possui dois pontos em que a derivada é zero e a função possui valor zero na mesma coordenada de tempo. Logo a função é a derivada de .

Já a curva possui um ponto em que a derivada é igual a zero e a função A assume o valor zero na mesma coordenada. Então é a derivada de .

Então é a função da posição.

Derivando ela temos a função , que é a velocidade.

E derivando novamente temos que é a aceleração.