Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.4 - Ex. 18ab
18. A figura a seguir mostra a velocidade v = f(t) de uma partícula que se movimenta ao longo de uma reta coordenada horizontal.
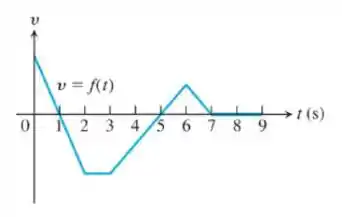
a. Quando a partícula se move para a frente? E para trás? Quando acelera? Quando desacelera?
b. Quando a aceleração da partícula é positiva? E quando é negativa? E nula?
c. Quando a partícula se move à velocidade máxima?
d. Quando a partícula permanece parada por mais de um instante?
Passo 1
a.
Okay, estamos numa linha reta. Então as únicas duas direções possíveis são para frente e para tras. Esse detalhe é importante. Isso quer dizer que temos muitas maneiras de interpretar o gráfico. Eu gosto da ideia de usarmos o conceito de integral para isso. A integral da velocidade no tempo nós da o espaço percorrido
Isso é muito legal porque a integral, se vermos geometricamente são as áreas do gráfico. Então nosso espaço percorrido é positivo (PARA FRENTE) quando a área do gráfico for positiva. E isso é facilmente visível.
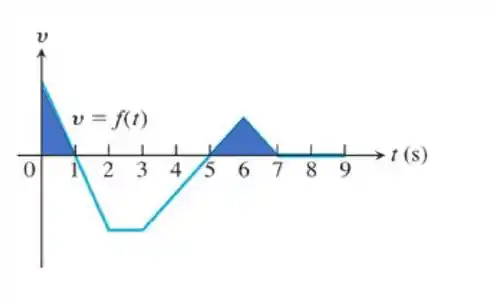
Pintei a região para deixar bem evidente. Então podemos dizer que a nossa partícula se move para frente em
A mesma logica pode ser usada para quando ela se move para tras. Emtão a partícula retorna em
Passo 2
B ) A aceleração já usa outro conceito bem visível também geometricamente, a derivada. Nossa aceleração é a derivada da velocidade no tempo
Podemos interpretar isso como ângulos de retas. A aceleração sera positiva quando a reta apontar para cima. Então estamos acelerando em
E sera negativa quando a reta apaontar para baixo. E isso acontece nos intervalos de
Se a reta tem ângulo zero, nossa derivada também sera zero. Logo
Quando
.
E isso acontece nos intervalos de
Resposta
A. Frente: e .
Trás: .
Acelera: .
Desacelera: e .
B. Positiva: .
Negativa: e .
Nula: e .