Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 14
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano . Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar conforme a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.
14.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
No início da tarefa, vamos expressar o parâmetro das variáveis e para eliminá-lo. Se elevarmos ao quadrado as expressões onde aparecem as variáveis e , obtemos:
Se nós incluímos a equação (2) na (1), obtemos que
A equação (3) representa a equação de uma hipérbole com vértices nos pontos . Os ramos da parábola são simétricos em relação a .
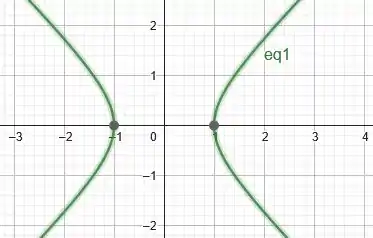
Passo 2
A variável é definida como . Como a segunda raiz é não negativa, assume valores maiores ou iguais a 0. A partir dessa condição, concluímos que a partícula se move ao longo da parte da hipérbole localizada acima do eixo . Da mesma forma, a variável é definida como . Como é não negativo, o menor valor que assume é para , ou seja,
Devido a condição que , concluímos que estamos olhando apenas para a parte da hipérbole que está no primeiro quadrante.
Passo 3
Se desenharmos esses pontos na hipérbole, obtemos a direção do movimento da partícula:
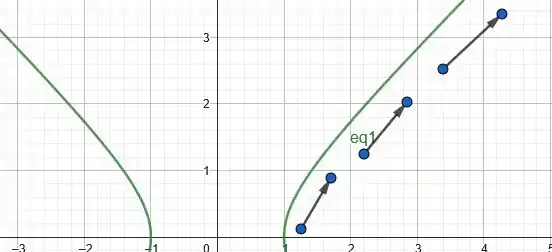
Determinamos a direção do movimento da partícula para que as setas passassem de valores menores do parâmetro para valores maiores.