Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 18
a) Elimine o parâmetro para encontrar uma equação cartesiana da curva.
b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Veja meu nobre amigo, temos a curva parametrizada:
O problema fornece essa curva na forma parametrizada e pede para encontrarmos uma equação cartesiana que relacione e .
Quando queremos eliminar um parâmetro de uma equação paramétrica, devemos isolar um termo semelhantes as duas equações, e então deveremos substituir na outra equação.
E é isso que iremos fazer aqui.
Para gerar o gráfico da reta, a gente vai utilizar uma ferramenta gráfica. Aqui a gente vai utilizar o GeoGebra para construir o gráfico. Outra forma de se construir o gráfico, é utilizar de uma tabela, escolhe-se pontos de e encontramos os pontos respectivos de e .
Passo 2
Neste caso, temos
Isolando na primeira equação:
Logo,
Portanto, a equação cartesiana da curva é a reta . Todavia, como
temos que
Assim, apenas um trecho da reta deve ser considerado...
Passo 3
Fazendo um esboço da curva...
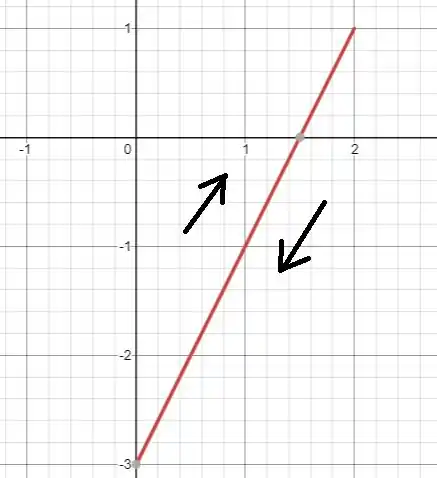
Como é periódica, a parametrização vai ficar oscilando (indo e vindo) sobre a reta.