Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 11
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano . Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar conforme a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.
11.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
No início da tarefa, observe como podemos escrever como:
Sabemos pelas condições da tarefa que é igual a , portanto, se incluirmos esse fato na equação (1), obtemos:
A equação dada é a equação do polinômio cúbico. As coordenadas da posição da partícula satisfazem a equação , então a partícula se move ao longo do polinômio cúbico.
Pelas condições do problema, sabemos que t pode ser qualquer número real. Por causa de , assume valores dentro do intervalo independentemente do valor que tomamos para o parâmetro t, ou seja,
Por esta razão, desenhamos o polinômio cúbico como uma função
Apenas para .
Passo 2
Se plotarmos os pontos no sistema de coordenadas, obtemos a seguinte função cúbica:
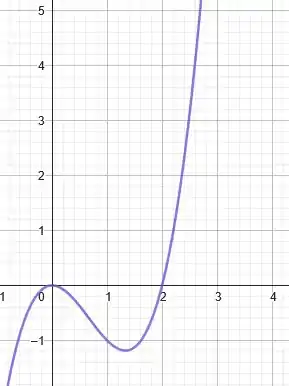
Se é negativo e se aproxima de zero, então a partícula se aproxima da origem, e se é positivo, à medida que aumenta, a partícula se afasta cada vez mais da origem.