Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 10

Aplique o método de Newton a f x = x 1 3 com x 0   =   1 e calcule x 1   ,   x 2 ,   x 3   e   x 4 . Determine uma fórmula para x n . O que acontece com x n quando n → ∞ ? Desenhe uma figura que mostre o que ocorre.

Passo 1

Para a função dada precisamos calcular o valor de x 1   ,   x 2 ,   x 3   e   x 4 e achar uma fórmula geral para x n utilizando o método de Newton que nos diz que

x n + 1 = x n - f ( x n ) f ' ( x n )           ( i )

e dizer o que acontece quando o valor de n tende a infinito.

Passo 2

Primeiramente, vamos derivar nossa função f ( x ) para depois aplicarmos o método de Newton

f x = x 1 3   → f ' x = 1 3 ⋅ x - 2 3

Dessa forma, aplicando a fórmula do método de Newton para o nosso caso, obteremos

x n + 1 = x n - x n 1 3 1 3 ⋅ x n - 2 3          

x n + 1 = x n - x n 1 3 - - 2 3 1 3      

x n + 1 = x n - 3 x n 1 3 + 2 3      

x n + 1 = x n - 3 x n 3 3

x n + 1 = x n - 3 x n

x n + 1 = - 2 x n

Passo 3

Para calcularmos x 1 utilizaremos o valor de x 0   dado

x 0 + 1 = - 2 x 0

x 1 = - 2 ⋅ 1 =   - 2

Seguindo o mesmo raciocínio, podemos fazer

x 1 + 1 = - 2 x 1

x 2 = - 2 x 1 = - 2 ⋅ - 2 = 4

x 2 + 1 = - 2 x 2

x 3 = - 2 ⋅ x 2

x 3 = - 2 ⋅ 4 =   - 8

x 4 = - 2 ⋅ x 3

x 4 = - 2 ⋅ - 8 = 16

Passo 4

Dessa forma, podemos generalizar para qualquer termo e obteremos

x n + 1 = - 2 x n

x n + 1 = 2 ⋅ x n

∴ x n + 1 2 = x n

Ou ainda podemos reindexar e obteremos

x n = - 2 x n - 1

∴ x n = 2 ⋅ x n - 1

Observamos que quando n → ∞ isso implica x n → ∞

Passo 5

O que ocorre quando n → ∞ pode ser ilustrado na figura abaixo

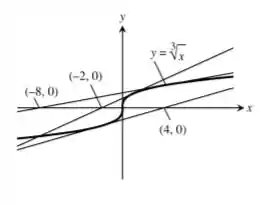
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método de Newton para estimar as duas raízes da função f ( x )=x 4+x-3 . Comece com x 0=- 1 para a raiz à esquerda e depois com x 0=1 para a raiz à direita. Então, determine x 2 em cada caso.
Demonstre que, se h0 , aplicando o método de Newton para f x = x ,x ≥ 0 - x ,x0 que leva a x 1=-h se x 0=h e a x 1=h se x 0=-h . Desenhe uma figura que mostre o que ocorre.
A curva y=t gx cruza a reta y=2 x entre x=0 e x = π 2 . Use o método de Newton para determinar onde isso ocorre.
Use o método de Newton para estimar as duas raízes da função f ( x )=2 x-x 2+1 . Comece com x 0=0 para a raiz à esquerda e depois com x 0=2 para a raiz à direita. Então, determine x 2 em cada caso
Use o método de Newton para estimar as soluções da equação x 2 + x - 1 = 0 . Comece comx 0=-1 para a solução à esquerda e com x 0=1 para a solução à direita. Depois, determine x 2 em cada caso.