Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 24

Para que valor(es) de x teremos ln (1 - x^2) = x - 1 ?

Passo 1

Para obtermos ln (1 - x^2) = x - 1 separaremos em duas funções e vamos plotar o gráfico para ver o ponto de intersecção entre eles. Dessa forma, tomemos y 1 = ln (1 - x^2) e y 2 = x - 1 , plotando o gráfico vamos obter

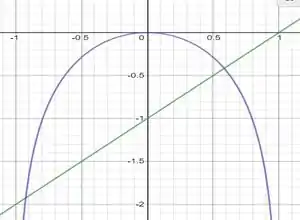
Observamos 2 valores de x para os quais as funções se encontram, utilizando o método de Newton para aproximação de raízes vamos precisar de 2 valores iniciais para aproximação de raízes, sendo assim, vamos pegar como valores iniciais - 0 . 9 e 0.5 que estão próximos dos pontos de encontro como é possível observar pelo gráfico. Lembrando que o método de Newton nos diz que

x_n + 1 = x_n - (f ( x_n ))/(f ' ( x_n ))

Passo 2

Primeiramente vamos derivar a função, para poder substituir na fórmula do método de Newton. Assim,

f (x) = ln (1 - x^2) - x + 1 -> f^' (x) = - (2 x)/(1 - x^2) - 1

Assim,

x_0 + 1 = x_0 - (f ( x_0 ))/(f ' ( x_0 ))

x_1 = x_0 - (ln (1 - x_0^2) - x_0 + 1)/(- (2 x_0)/(1 - x_0^2) - 1)

Na ordem dos pontos iniciais vamos pegar primeiro x_0 = - 0 . 9 e obteremos

x_1 = x_0 - (ln (1 - x_0^2) - x_0 + 1)/(- (2 x_0)/(1 - x_0^2) - 1)

x_1 = - 0.9 + (ln (1 - (0.9)^2) + 0.9 + 1)/((2 * (- 0.9))/(1 - (0.9)^2) + 1)

x_1 tildetilde - 0.92824

Agora, para x_0 = 0.5 5

x_1 = x_0 - (ln (1 - x_0^2) - x_0 + 1)/(- (2 x_0)/(1 - x_0^2) - 1)

x_1 = 0.55 + (ln (1 - ( 0.55 )^2) - ( 0.55 ) + 1)/((2 * (0.55))/(1 - ( 0.55 )^2) + 1)

x_1 tildetilde 0,584825

Resposta

x tildetilde - 0.92824 o u x tildetilde 0,584825

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aplique o método de Newton a f x = x 1 3 com x 0=1 e calcule x 1,x 2 ,x 3ex 4 . Determine uma fórmula para x n . O que acontece com x n quando n → ∞ ? Desenhe uma figura que mostre o que ocorre.
As curvas y=x 2 ( x+1 ) e y= 1 x( x0 ) se cruzam em um ponto x=r . Use o método de Newton para estimar o valor de r com quatro casas decimais.
A figura a seguir mostra um círculo de raio r com uma corda de comprimento 2 e um arco s de comprimento 3 . Use o método de Newton para resolverr e θ (radianos) com quatro casas decimais. Suponha que
Para que valor(es) de x obteremos c o s (x) = - x ?