Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 11
Nos exercícios 8 a 14, obter uma equação cartesiana para a superfície dada. Representá-la graficamente.
Passo 1
Para resolver, vamos utilizar o método da seção 10.2.9. Vamos substituir os elementos livres e por e :
Logo:
Passo 2
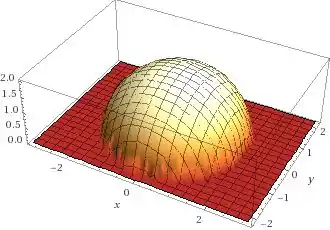
Note que se esta é a equação do topo de uma esfera
Resposta
Exercícios de Livros Relacionados
Identifique a superfície que tem a equação paramétrica dada. r → u , v = u + v i → + 3 - v j → + 1 + 4 u + 5 v k →
Determine se os pontos P e Q estão na superfície dada r → u , v = u + v ,u 2 - v ,u + v 2 P 3 , - 1,5 ,Q ( - 1,3 , 4 )
Determine se os pontos P e Q estão na superfície dada r → u , v = 2 u + 3 v ,1 + 5 u - v ,2 + u + v P 7,10,4 ,Q ( 5,22,5 )
Identifique a superfície que tem a equação paramétrica dada. r s , t = s , t , t 2 - s 2
Identifique a superfície que tem a equação paramétrica dada. r s , t = ss e n2 t , s 2 , scos 2 t