Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 24

Nos exercícios de 21 a 24, a região é limitada pelas curvas x = y 2 - 2   e   x = 6 - y 2   gira em torno do eixo indicado. Ache o volume do sólido gerado.

24.a reta y = 2

Passo 1

Primeiro vamos usar a figura abaixo para entendermos como as duas curvas se comportam e onde o eixo da questão está (o gráfico é y em função de x, ou seja, y vertical e x horizontal):

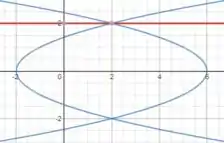
Pela equação de invólucro cilíndrico, nosso volume será:

V = 2 π ∫ a b x f x d x

Passo 2

Bom, como queremos rotacionar toda a região interna entre as duas curvas, vamos subtrair uma função da outra para podermos integrar apenas a parte interna:

f y = 6 - y 2 - y 2 - 2 = 8 - 2 y 2

Essa será nossa função que iremos substituir na equação. Para escrevermos o x que está multiplicando f(x), precisaremos substitui-lo por 2 - y para que a rotação ocorra no eixo y = 2 .

Nossa equação então vai ficar:

V = 2 π ∫ a b 2 - y 8 - 2 y 2 d y

Como y vai de -2 até 2 na região interna, os limites então serão:

V = 2 π ∫ - 2 2 2 - y 8 - 2 y 2 d y

Passo 3

Agora vamos resolver a integral:

V = 2 π ∫ - 2 2 2 - y 8 - 2 y 2 d y

Reescrevendo:

V = 2 π ∫ - 2 2 16 - 8 y - 4 y 2 + 2 y 3 d y

Integrando cada termo:

V = 2 π 16 y - 4 y - 4 3 y 2 + 1 2 y 4 2 - 2

Aplicando os limites de integração:

V = 256 π 3

Resposta

V = 256 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

10 - Determine o volume do sólido gerado pela rotação da região limitada pela parábola y 2=4 x e pela reta y=x em torno:Do eixo xDo eixo yDa reta x = 4Da reta y = 4
10 - Determine o volume do sólido gerado pela rotação da região limitada pela parábola y 2=4 x e pela reta y=x em torno:Do eixo xDo eixo yDa reta x = 4Da reta y = 4
10 - Determine o volume do sólido gerado pela rotação da região limitada pela parábola y 2=4 x e pela reta y=x em torno:Do eixo xDo eixo yDa reta x = 4Da reta y = 4
10 - Determine o volume do sólido gerado pela rotação da região limitada pela parábola y 2=4 x e pela reta y=x em torno:Do eixo xDo eixo yDa reta x = 4Da reta y = 4
Uma esfera de raio 10 cm é interceptada por dois planos paralelos do mesmo lado do centro da esfera. A distância do centro da esfera a um dos planos é 1 cm e a distância entre os planos é 6 cm. Ache o