Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 89
Nós exercícios 89 e 90, são dados uma função f e um intervalo fechado [a,b]. Verifique se o teorema do valor intermediário é aplicável para o valor dado de k e ache um número c tal que . Faça um esboço da curva e reta
89)
Passo 1
A questão solicita que se verifica a aplicação do teorema do valor intermediário para k=10 no intervalo [2,4].
Como f é uma função polinomial, será contínua em toda parte. Uma vez que , o teorema do valor intermediário garante que existe um número c entre 2 e 4 tal que
Substituindo teremos,
Rejeitamos pois esta fora do intervalo [2,4]. Portanto
Passo 2
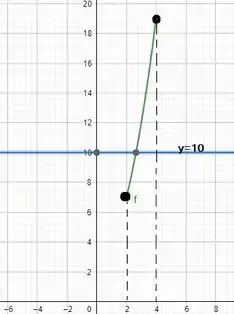
O esboço da curva e da reta estão apresentados abaixo:
Resposta
O teorema do valor intermediário se aplica para k=10 no intervalo [2,4], sendo .
Gráfico:
Exercícios de Livros Relacionados
Use o teorema do valor intermediário nos Exercícios 71 -78 para provar que cada equação tem uma solução. Em seguida, utilize uma calculadora gráfica ou um computador com software gráfico para resolver
Prove que a equação tem pelo menos uma raiz real. (b) Use recursos gráficos para encontrar a raiz correta até a terceira casa decimal53. x 5 - x 2 - 4 = 0
Para quais valores da constante c a funçãof é contínua em - ∞ , ∞ ? f ( x ) = c x + 1,s ex ≤ 3 c x 2 - 1 ,s ex3
Use o Teorema do valor intermediário para provar que existe um número c positivo tal que seu quadrado é igual c 2 = 2 .(Isso prova a existência do número 2 )
Se f ( x ) =x 3 - x 2 + x , mostre que existe um número c tal que f ( c ) = 10