1. Prove que a equação tem pelo menos uma raiz real. (b) Use recursos gráficos para encontrar a raiz correta até a terceira casa decimal

53.

A função , é contínua em todo o seu domínio. Isso acontece, pois, nossa função é um polinômio, e todos os polinômios são contínuos em todo o seu domínio.

Nosso objetivo então é descobrir dois valores de tais que o esteja entre eles:

Então, o nosso objetivo é encontrar tal que:

Isso quer dizer que precisamos de um ponto da função menor que zero e outro ponto maior que zero.

Veja a nossa função, ela tem um termo elevado a potência, ele termo irá crescer substancialmente mais que os outros termos da função, sendo assim, não é difícil encontrarmos um ponto maior que zero.

Vamos testar para :

Agora vamos pensar em um valor menor do que zero. Veja que o nosso termo elevado a quinta potência é um termo ímpar, sendo assim, ao elevarmos um valor negativo a uma potência ímpar teremos um valor negativo, e agora termo a quinta potência irá diminuir muito mais rapidamente do que os outros termos da função.

Vamos testar para :

Então encontramos nossos pontos, sendo assim, temos um raiz real entre esses pontos.

Quando e , temos um intervalo em que o está contido entre eles, como é contínua, podemos afirmar que existe um valor para o qual , e esse valor está entre

Utilizando do GeoGebra, vamos encontrar a raiz:

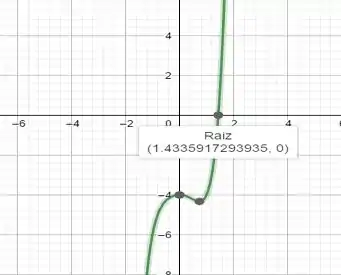
Raiz, pelo método gráfico é