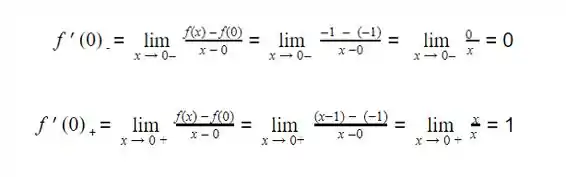Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 5c
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em ; (c) calcule e se existirem; (d) determine se é derivável em.
Letra (c)
Passo 1
Nesta letra ele nos pede para determinar a derivada à esquerda e à direita de f (x) em x1 = 0.
A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
Passo 2
A derivada à esquerda de f(X) em x1 = 0 será:
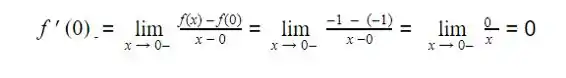
Passo 3
A derivada à direita de f(X) em x1 = 0 será :
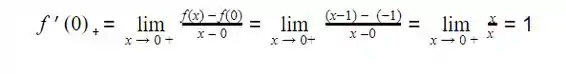
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 25 a 30, ache f ' ( x ) aplicando a fórmula (3).25) f x = 7 x + 3
Nos Exercícios de 25 a 30, ache f ' ( x ) aplicando a fórmula (3).27) f x = - 4
Nos Exercícios de 25 a 30, ache f ' ( x ) aplicando a fórmula (3).30) f x = 3 x 2 - 2 x + 1
Nos Exercícios de 25 a 30, ache f ' ( x ) aplicando a fórmula (3).29) f x = 4 - 2 x 2
Nos Exercícios de 25 a 30, ache f ' ( x ) aplicando a fórmula (3).28) f x = 3 x 2 + 4