Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.8 - Ex. 1a
Explique por que cada uma das seguintes integrais é imprópria.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente explicar por que a integral da função , no intervalo , é imprópria.
Pra isso, primeiro a gente precisa lembrar que integrais impróprias são aquelas em que pelo menos uma extremidade do intervalo é estendida até o infinito. E isso geralmente acontece quando temos alguma indeterminação na nossa função, ou seja, valores de para os quais a função não estará definida em seu domínio.
O fato de termos um quociente já nos dá uma boa dica para encontrar esses valores, porque a gente sabe que o denominador de uma função nunca pode ser zero.
Então, com base nisso, vamos lá avaliar nossa função!
Passo 2
Nossa função é dada por:
Se o denominador não pode ser zero, temos:
E isolando :
Isso quer dizer que a nossa função tem uma singularidade em , ou seja, ela não está definida para este valor. Olha só o que acontece no gráfico da função:
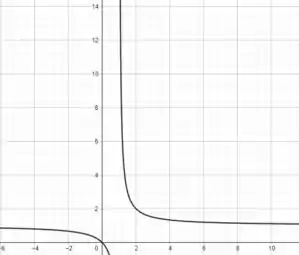
Repare que ela possui uma assíntota vertical em , uma reta que se prolonga até o infinito sempre nesse ponto. Isso quer dizer, uma das extremidades do intervalo de integração de se prolonga até o infinito:
Por termos essa descontinuidade infinita em , essa integral é dada como integral imprópria do tipo 2.
Valeu, galera! Até a próxima! 😉