Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.5 - Ex. 8

  1. Explique por que a função cujo gráfico é mostrado é uma função densidade de probabilidade.
  2. Use o gráfico para encontrar as seguintes probabilidades:
    1. P ( X < 3 )
    2. P ( 3 ≤ X ≤ 8 )
  3. Calcule a média.

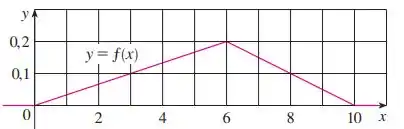
Passo 1

  1. Como no exercício anterior, as condições que nós temos é
    1. f x ≥ 0
    2. ∫ - ∞ ∞ f ( x ) d x = ∫ 0 10 f ( x ) d x = 1 2 10 0.2 = 1 (isso representa a área do triângulo da figura. Assim f ( x ) representa uma função densidade de probabilidade.

    Passo 2

  2. (i) Para achar pelo gráfico, nós só precisamos encontrar a área do triângulo “atrás” de x = 3 , então, P X < 3 = ∫ 0 3 f ( x ) d x = 3 0.1 2 = 0.15 .

    3. (ii) Nós já temos a área total, e a área da probabilidade de x < 3 , então, achando a probabilidade de x > 8 , nós conseguimos achar a probabilidade desse item. Então, P X > 8 = ∫ 8 10 f ( x ) d x = 2 0.1 2 = 0.1 . Logo, P 3 ≤ X ≤ 8 = 1 - P X < 3 - P X > 8 = 1 - 0.15 - 0.1 = 0.75 .

    Passo 3

  3. Nós encontramos as equações da reta para ( 0,0 ) a ( 6 ,   0.2 ) , e para ( 6 ,   0.2 ) a ( 10 ,   0 ) , e encontramos que

f x = 1 30 x   s e   0 ≤ x < 6 - 1 20 x + 1 2   s e   6 ≤ x < 10 0   e m   o u t r o s   c a s o s

Assim, nossa média é

μ = ∫ - ∞ ∞ x   f x   d x = ∫ 0 6 x 1 30 x d x + ∫ 6 10 x - 1 20 x + 1 2 d x =

1 90 x 3 0 6 + - 1 60 x 3 + 1 4 x 2 6 10 = 216 90 + - 1000 60 + 100 4 - - 216 60 + 36 4 =

16 3 = 5 . 3 -

Resposta

  1. f ( x ) representa uma função densidade de probabilidade
  2. (i) 0.15

    3. (ii) 0.75

  3. 5 . 3 -
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais impróprias.
Nos exercícios de 1 a 25, determine se a integral imprópria é convergente ou divergente. Se for convergente, calcule-a.5. ∫ 2 4 d t 16 - t ² ²
Determine se cada integral é convergente ou divergente. Calcule a convergente ∫ 3 ∞1 x - 2 3 2 d x
Determine se cada integral é convergente ou divergente. Calcule a convergente ∫ - ∞ ∞ cos ⁡ π td t
Determine se cada integral é convergente ou divergente. Calcule a convergente ∫ - ∞ 0ze 2 zd z