Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.2 - Ex. 7
Dê exemplo de uma função definida em e que seja contínua em todos os pontos exceto nos inteiros.
Passo 1
Faaaala aí, tudo bem? Vamos resolver essa questão!
O enunciado pediu pra gente dar um exemplo de uma função, que seja definida no conjunto dos números reais e contínua em todos os pontos, exceto nos números inteiros.
Só para relembrar galera, um número inteiro é aquele que não tem vírgula e não precisa ser escrito na forma de fração. Por exemplo:
E pra lembrar também da definição, uma função é dita contínua em um ponto se:
Com base nisso, vamos construir a nossa função. Vamos lá!
Passo 2
A questão pede da gente uma função que é contínua em todos os pontos menos nos inteiros. Veja bem, o exercício não pede necessariamente que você encontre uma função exata. Então vamos começar esboçando um gráfico qualquer:
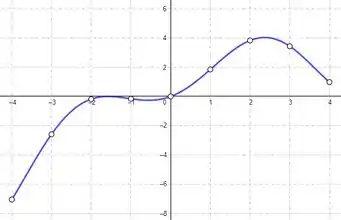
Repara que marcamos alguns pontos com bolinhas brancas. Estes pontos são justamente os números inteiros e essas bolinhas brancas estão dizendo que a função não esta definida naquele ponto, ok?
Mas podemos melhorar essa resposta!
Passo 3
Agora vamos tentar dar uma fórmula qualquer para essa função. Lembra que qualquer polinômio de grau é contínuo em todos os pontos. Portanto, uma baseada em pode ser escrita como:
Por exemplo:
Dessa forma, é igual a qualquer número negativo quando . Ou seja, a função existe para todos os pontos menos para os números inteiros.
Valeu, galera! Até a próxima! 😉