Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 19
Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
O enunciado fornece uma função e um ponto e pede para justificarmos o motivo de não ser contínua nesse ponto.
Relembrando, para uma função ser contínua em um ponto ela deve estar definida neste ponto e além disso, o valor da função neste ponto deve coincidir com o valor do limite (que deve existir). Desta forma, devemos calcular tanto o valor do limite como da função no ponto considerado e compará-los!!!
Passo 2
Primeiramente, em casos de continuidade devemos analisar o domínio da função que queremos analisar. Como tanto a exponencial como o polinômio não tem restrições quanto ao domínio, a função está definida na reta real toda.
Passo 3
Vamos calcular o limite de quando tende a . Como a a função à direita de é diferente da função à esquerda, devemos calcular os limites laterais. O limite à esquerda é:
O limite à direita é
Os limites laterais são diferentes e, portanto, o limite não existe e deste modo a função não é contínua nesse ponto.
Passo 4
O esboço do gráfico da função é gerado utilizando GeoGebra:
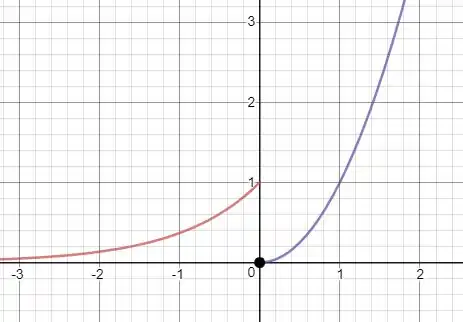
Uma outra forma de se notar a descontinuidade de uma função é analisando o seu gráfico. A função é continua se não houver descontinuidades abruptas, como saltos, buracos, ou assíntotas verticais
Resposta
R: demonstração e esboço de gráfico.