Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 31
Explique por que o método de Newton não funciona para encontrar as raízes da equação se o valor inicial escolhido for .
Passo 1
Faala ae... nessa questão temos a seguinte equação
E devemos explicar por que que o método de Newton não funciona para encontrar as raízes dessa equação usando o valor inicial de
Bom, o método de Newton é um método iterativo, onde a partir de um chute inicial , encontramos novos valores para a raiz a partir da seguinte fórmula iterativa:
Esses novos valores são obtidos a partir da reta tangente a função no ponto atual. Geometricamente, o que temos é algo mais ou menos assim:
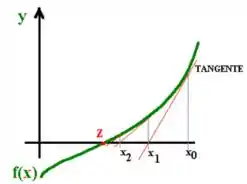
Esse método não funciona quando os novos valores não se aproximam da raíz da função, isso é, o método pode acabar divergindo. Motivos para isso ocorrer são quando a derivada te leva a valores que te afastam da raíz.
Dessa forma, vamos tentar usar o método de Newton nessa função e ver o que ocorre.
Passo 2
Primeiro temos que
Vamos agora precisar de , vamos calcular então!!
Para achar a derivada de vamos usar algumas regras de derivação, o da função constante e do polinômio:
Vamos calcular :
Passo 3
Pronto, agora que temos é só jogar na fórmula de Newton:
Vamos usar , como pedido na questão, agora é só substituir, vamos lá:
Não é possível calcular , pois com temos que , e a linha tangente usada para aproximar é horizontal, e como dá pra ver na expressão acima, tentar calcular resulta em tentar dividir por .
Resposta
Não é possível calcular , pois com temos que , e a linha tangente usada para aproximar é horizontal, e como dá pra ver na expressão acima, tentar calcular resulta em tentar dividir por .