A tabela fornece a população do México (em milhões) em anos de censo no século XX.
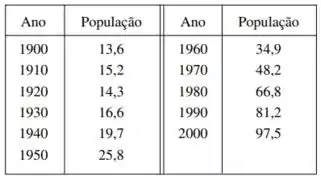
a) Usa uma calculadora gráfica ou um computador para ajustar uma função com os dados. Faça um gráfico dos pontos dados e do modelo exponencial. Quão bom é o ajuste?
b) Estime as taxas de crescimento populacional em 1950 e 1960 fazendo a média de inclinações de retas secantes.
c) Use a exponencial da parte (a) para encontrar um modelo para as taxas de crescimento da população do México no século XX.
d) Use seu modelo na parte (c) para estimar as taxas de crescimento em 1950 e 1960. Compare com sua estimativa da parte (b).
Passo 1
Eaee, belezinha???
Bom...Assim como na questão 85, aqui devemos fazer um ajuste de uma função exponencial aos dados fornecidos da população do México (em milhões) no decorrer dos anos:
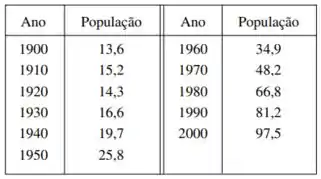
Para isso, vamos tentar ajustar uma função do tipo .
A taxa de crescimento será a derivada temporal de , isto é, .
Além disso, no item (b) devemos calcular as derivadas numericamente usando inclinações de retas secantes.
Passo 2
Fazendo um ajuste no computador usando o método dos mínimos quadrados, obtivemos:
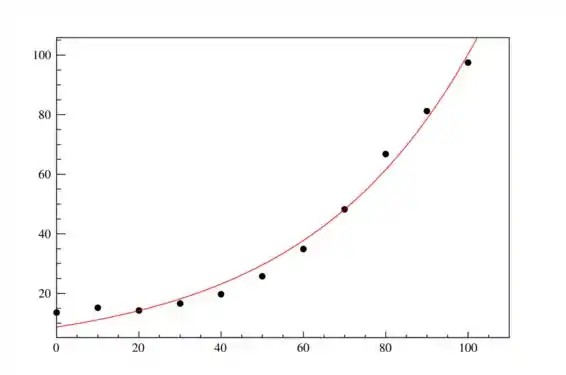
Para simplificar, usamos uma escala para de a , assim, 1900 corresponde a , 1910 a , e assim por diante, até 2000 que equivale a .
Vale notar que o ajuste por uma função exponencial não passa rigorosamente por todos os pontos, todavia, para um modelo simples ele é bem aceitável.
Os valores obtidos para e foram e . Assim:
Passo 3
Queremos agora estimar as derivadas de em 1950 ( e 1960 ( usando retas secantes.
Para isso, vamos usar a definição de coeficiente angular de reta, de modo que a derivada pode ser estimada por
Consideremos que a reta passa por e por .
Assim, para 1950:
Para 1960:
Passo 4
Usando o modelo exponencial, basta derivar que encontramos uma expressão para a taxa de crescimento em função do tempo:
Como e , temos:
Passo 5
Vamos usar o modelo obtido para para calcular a taxa de crescimento em 1950 e 1960:
Comparando estes resultados com o método da secante, vemos que para 1950 obtivemos resultados próximos, porém para 1960 eles foram bem discrepantes.
Resposta
a)
b) e
c)
d) e