Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.5 - Ex. 36

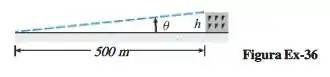
Suponha que, medido a 500 m da base de sua base, o ângulo de elevação do alto de um edifício seja θ = 6 º .   (Ver figura dada.) Use uma aproximação linear local junto a algumas contas mentais para mostrar que o edifício tem aproximadamente 52 m de altura.

Passo 1

Nessa questão vale lembrar que o seno representa o cateto oposto dividido pela hipotenusa, certo? Onde nesse caso o cateto oposto é justamente a altura h do prédio que estamos procurando.

A aproximação linear local que conhecemos fica:

f x ≈ f x 0 + f ' x 0 x - x 0

Onde nosso f x = s e n   x   e   x 0 = 0 ,   já que o sen0 é o valor mais próximo conhecido.

Passo 2

Nossa aproximação fica então:

f x ≈ s e n   0 + cos ⁡ 0   ( x - 0 )

f x ≈ x

f 6 = s e n 6 ≈ 6 º

f 6 ≈ π 30

Passo 3

Lembrando a relação trigonométrica temos então:

c a t e t o   o p o s t o h h i p o t e n u s a ≈ π 30  

c a t e t o   o p o s t o   h ≈ π 500 30

h = 52,35

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 17 a 24, ache d y . y = 2 + c o s x 2 - s e n x
Nos exercícios de 25 a 30, x e y são funções de uma terceira variável. Calcule d y d x , encontrando o diferencial termo a termo (veja o Exemplo 3). s e n x c o s y - c o s x s e n y = 1 2
Nos exercícios de 17 a 24, ache d y . y = x 2 s e n 1 x - x c o s 1 x
y = x ;x = 4eΔ x = 3 Encontre d y e Δ y para os valores indicados de x e Δ x .Faça um esboço do gráfico e indique os segmentos de reta cujos comprimentos são d y e Δ y .
y = x 3 ;x = 2eΔ x = 1 Encontre d y e Δ y para os valores indicados de x e Δ x .Faça um esboço do gráfico e indique os segmentos de reta cujos comprimentos são d y e Δ y .