Explique como podem ser obtidas as assíntotas de a partir das assíntotas curvilíneas de e .

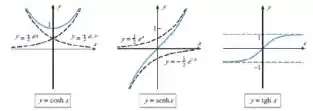
Bom galera, sabemos que as duas funções hiperbólicas que geram as outras as quais conhecemos (secante, cossecante, etc), são a e . As quais possuem assíntotas curvilíneas, para temos e . Já para , temos e .

A função é determinada pela razão:

Por esse motivo temos que as assíntotas da tangente hiperbólica podem ser obtidas pelo cosseno e seno hiperbólicos.