Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 19
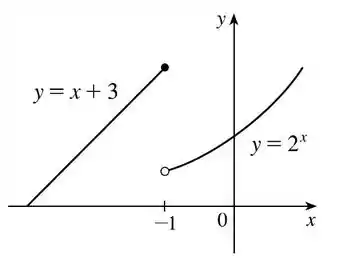
Explique porque a função é descontínua no número dado . Desenho o gráfico da função.
Passo 1
Nesse exercício iremos analisar a função:
No ponto:
Em relação a sua discontinuidade.
Para que o limite da função seja continua, devemos ter:
Isso é, o limite da função e a imagem da função deve ser o mesmo no ponto dado.
Passo 2
Iremos calcular os limites laterais de , sendo assim:
E:
Dessa forma, podemos afirmar que não existe e é descontínua no ponto -1.
Passo 3
Podemos verificar o que foi posto no passo 2 através da análise do gráfico da função a seguir:
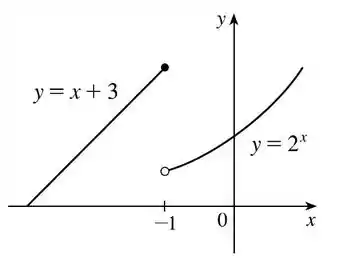
Resposta
Exercícios de Livros Relacionados
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua. f x = 2
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua.f x = x + 1
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua. f x = x 2s ex ≤ 1 2s ex1
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua.f x = x 2
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua. f x = 1 x 2s ex ≥ 12s ex1