Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 1e
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua.
Passo 1
Opa! Vamos resolver essa questão! Aqui temos que esboçar o gráfico da função dada usando a ideia intuitiva de função contínua :
Beleza, mas o que é uma função contínua?!
Uma função é contínua se você conseguir pegar um lápis e desenha-la no papel sem tirar o lápis do papel! Mas isso tem que valer pra todo , se tiver algum em que você precise dar uma levantadinha então a função já não é contínua! Sacou?!
Passo 2
Com nossa função é
Ou seja:
E
O gráfico de é dado pela reta para valores de entre e e por para os demais valores.
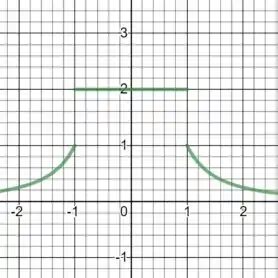
Assim, nossa função, apresenta dois saltos: um em e outro em . Então a função é cont��nua em todo real exceto em e em .
Podemos então dizer que:
é contínua para todo e .
Resposta
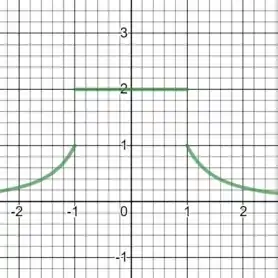
é contínua para todo e .