Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 17
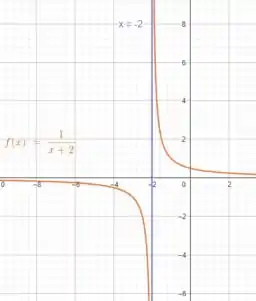
Explique porque a função é descontínua no número dado . Esboce o gráfico da função.
Passo 1
Eaee, belezinha?? Bom... queremos verificar o porquê dessa função ser descontínua quando (quando tende a ):
Para resolver isso, temos que imaginar o que acontece quando fazemos nessa função.
E aí?? Bora lá?? 😉
Passo 2
Bom... se liga quando fazemos :
Eita... temos uma indeterminação!!
Então podemos concluir que a função é descontínua em porque é indefinida!!
Passo 3
Agora vamos plotar essa função.
Bom... a gente sabe que a função é dada da seguinte forma:
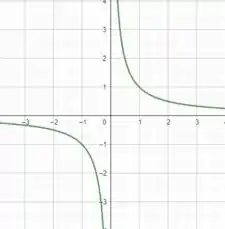
Agora a gente só desloca em duas unidades para esquerda para obtermos :
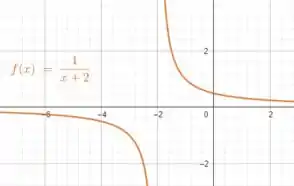
Vamos colocar uma reta em :
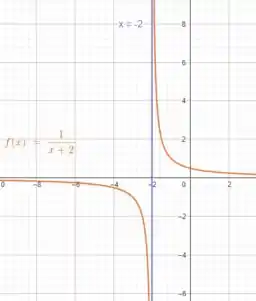
Perceba que quanto mais tendemos a , mais a função tende ao infinito!!
Resposta
A função é descontínua em porque é indefinida.
Exercícios de Livros Relacionados
Seja f x = x 5 + x + 1 . Justifique a afirmação: f tem pelo menos uma raiz no intervalo - 1,0 .
Prove que a equação x 3 - 4 x + 2 = 0 admite três raízes reais distintas.
Seja α a menor raiz positiva da equação x 3 - 4 x + 2 = 0 . Determine os intervalos de amplitudes 1 2 , 1 4 e 1 8 que contenham α .
Seja f contínua em a ,b e tal que fa fb . Suponha que quaisquer que sejam s e t em a ,b , s ≠t⇒fs ≠ ft . Prove que f é estritamente crescente em a ,b .(Observação: f estritamente crescente em a ,b⇔∀
Suponha que f : 0,1 → R seja contínua, f 0 = 1 e que f x é racional para todo x em 0,1 . Prove que f x = 1 para todo x em 0,1 .