Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 20
Explique porque a função é descontínua no número dado . Desenho o gráfico da função.
Passo 1
Oi galera, tudo bem? O problema começa nos dando essa função definida por partes
E pede para explicar por que ela é descontínua em . E agora?
Bom, quando temos uma função definida por partes, para que ela seja contínua no ponto de ‘quebra’ os limites laterais precisam ser iguais!
Temos que em a função vale , então precisamos verificar se em torno desse ponto a outra parte da função também tende a 1! Usando limites!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nesse exercício iremos analisar a função:
No ponto:
E dizer se ela é contínua!
Para que o limite da função seja continua, devemos ter:
Isso é, o limite da função e a imagem da função deve ser o mesmo no ponto dado, no nosso caso! Certo?
Iremos calcular o limite da função no ponto , sendo assim, temos:
Substituindo por teremos uma indeterminação
Isso significa que precisamos fatorar essa função e simplificar! Assim vamos levantar a indeterminação!
Passo 3
Fatorando o denominador como a diferença de quadrados
E no nosso caso temos
E no numerador? Temos como fator comum! Colocando o termo em evidência no numerador, temos:
Aí substituindo no limite temos
Agora simplificanco o termo que aparece no numerador e no denominador, obtemos:
Beleza?
Passo 4
E, finalmente, levantada a indeterminação, podemos substituir o valor de :
No entanto, conforme fornecido no enunciado, , dessa forma é descontínua no ponto 1.
Passo 5
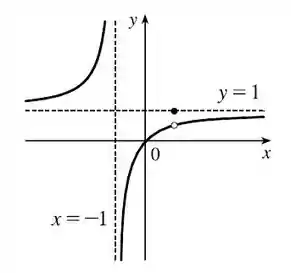
Podemos verificar o que foi posto no passo 2 através da análise do gráfico da função a seguir. Nossa função
Pode ser reescrita como
Que se comporta como uma hipérbole deslocada lateralmente em . E também deslocada verticalmente em uma unidade para cima!
Então o “novo” eixo seria em . E o “novo” eixo seria em .
Vamos ver o limite em torno de (ponto de quebra da função e descontinuidade) para ver seu comportamento!
Pela direita
E pela esquerda
Mas em a função vale , então na hipérbole veremos uma bolinha aberta!
Beleza?
Resposta
