Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 25
Explique, usando os teoremas 4, 5, 7 e 9, porque a função é contínua para qualquer número em seu domínio. Explicite o domínio.
Passo 1
Fala aí! como vai?
Nesse problema foi dada a função
E nosso objetivo é mostrar que a função é continua é todo seu domínio e tambem temos que determinar seu domínio.
Tem ideia de como fazemos isso?
Para resolver esse problema temos que usar os teoremas 4, 5, 7 e 9.
Pelo livro esses teoremas são
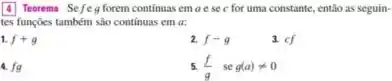
Veja só!
Passo 2
Perceba que nossa função é uma função racional entre dois polinômios, analisamos o comportamento do numerador e do denominador.
Se ambos forem contínuos e pelo teorema 4, , é continua em todo o domínio.
Como temos dois polinômios, sabemos que seus domínios não possuem restrições, então nos resta saber se o denominador assume um valor nulo.
O denominador é dado por
Perceba que independentemente do valor de , essa função sempre será diferente de , logo, não possui restrições no seu domínio e como visto no teorema 4, podemos afirmar que é continua em todo seu domínio.
E aí! entendeu tudo? Responde Aí!