Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 9

9. Expresse a área e o perímetro de um triângulo equilátero em função do comprimento x do lado do triângulo.

Passo 1

A área de um triâgulo qualquer é igual a sua base vezes a altura, belê? Só que como o triângulo é equilátero, já temos a base, que será x . Falta calcular sua altura:

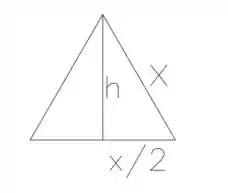
Fazendo Pitágoras:

x 2 = h 2 + x 2 2

h 2 = x 2 - x 2 2 = x 2 - x 2 4

h 2 = 4 x 2 4 - x 2 4 = 3 x 2 4

h = 3 x 2

A área então será:

A = b ∙ h 2

Sendo:

b = x

h = 3 x 2

Vamos ter:

A x = x ⋅ 3 x 2 2

A x = 3 x 2 4

Passo 2

Como o perímetro é a soma de todos os lados, e cada lado vale x , para calcularmos o perímetro basta fazer:

P x = x + x + x

P x = 3 x

Feshow

Resposta

A x = 3 x 2 4

P x = 3 x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Coloque na forma x - a 2 + y - b 2 = r 2 . x 2 + y 2 - 2 x = 0
Coloque na forma x - a 2 + y - b 2 = r 2 . x 2 + y 2 - x - y = 0
Um arame de 10 cm de comprimento deve ser cortado em dois pedaços, um dos quais será torcido de modo a formar um quadrado e o outro, a formar uma circunferência. De que modo deverá ser cortado para qu
Determine a equação da reta que passa pelo ponto dado e que seja perpendicular à reta dada. 3 x - 2 y = 0 e 0,0
Determine a equação da reta que passa pelo ponto dado e que seja paralela à reta dada. x - y = 2 e - 1,2