Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 33

Expresse a área A de um triângulo equilátero em função do lado l .

Passo 1

Temos que a área de um triângulo é dado por:

A = b ∙ h 2 = l ∙ h 2

Em um triângulo equilátero temos que os três lado são iguais, vamos então encontrar a altura e substituir na fórmula.

Passo 2

Pela figura abaixo vemos que temos um triângulo retângulo dentro do triângulo equilátero, e é da forma:

l 2 = 1 2 l 2 + h 2

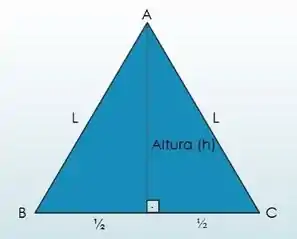
Vamos então isolar o h na expressão:

l 2 = 1 2 l 2 + h 2 ↔ h 2 = l 2 - 1 2 l 2 ↔ h = l 2 - 1 2 l 2 = l 2 - l 2 4 = 3 l 2 4 = l 2 3

Pronto, achamos que h = l 2 3 .

Passo 3

Agora é só substituir de volta na fórmula da área e pronto:

A = b ∙ h 2 = l ∙ h 2 = l ∙ l 2 3 2 = 3 4 l 2

Resposta

A = 3 4 l 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se o gráfico da função y= e - x 2 é simétrico em relação ao eixo x , à origem ou nenhum dos dois.
Determine se a função y = x - s e n x é par, ímpar, ou nenhuma das duas.
Determine se a função y = 1 - c o s x é par, ímpar, ou nenhuma das duas.
Determine se a função y = s e c xt g x é par, ímpar, ou nenhuma das duas.
Um balão de ar quente subindo a partir de um campo horizontal é rastreado por um telêmero localizado a 500 pés do ponto de decolagem. Expresse a altura do balão em função do ângulo que a reta faz com