Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 37

Expresse a equação:

x = 5 3 s e n 2 π t + 5 2 c o s ⁡ ( 2 π t )

Na forma x = A s e n ( ω t + θ ) e use um recurso gráfico para confirmar que ambas as equações têm o mesmo gráfico.

Passo 1

Cara, eu acredito que a questão esteja com erro e fosse:

x = 5 3 2 s e n 2 π t + 5 2 c o s ⁡ ( 2 π t )

Vamos abrir um pouquinho x = A s e n ( ω t + θ ) e comparar com x = 5 3 2 s e n 2 π t + 5 2 c o s ⁡ ( 2 π t ) depois.

Podemos fazer:

x = A s e n ω t + θ

x = A s e n ω t cos ⁡ θ + s e n θ cos ⁡ ω t

E em:

x = 5 3 2 s e n 2 π t + 5 2 cos ⁡ 2 π t

x = 5 3 2 s e n 2 π t + 1 2 cos ⁡ 2 π t

Opa, comparando as duas:

x = A s e n ω t cos ⁡ θ + s e n θ cos ⁡ ω t

x = 5 3 2 s e n 2 π t + 1 2 cos ⁡ 2 π t

Podemos dizer que:

A = 5

c o s ⁡ θ = 3 2

sen ⁡ θ = 1 2

Com isso, temos que θ = π 6 . E também temos:

s e n ω t = s e n ( 2 π t )

Logo, ω = 2 π . Com isso, já podemos montar a função:

x = 5 s e n 2 π t + π 6

Passo 2

Comparando os gráficos:

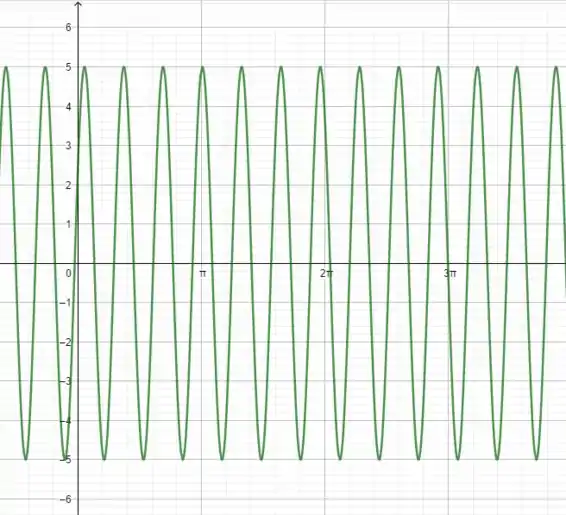
x = 5 s e n 2 π t + π 6

E x = 5 3 2 s e n 2 π t + 5 2 c o s ⁡ ( 2 π t ) :

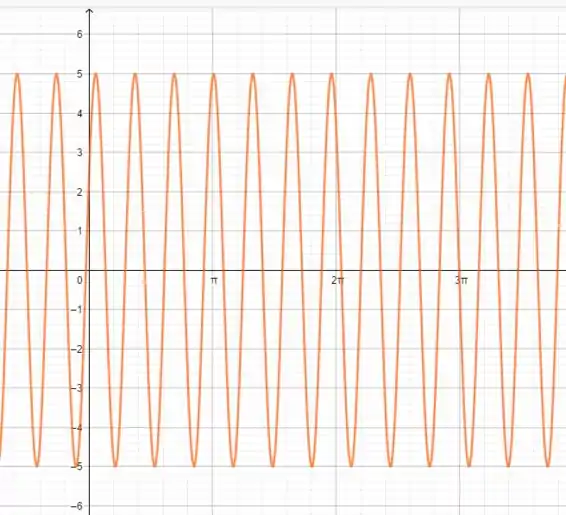
Certinho!

Resposta

x = 5 s e n 2 π t + π 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre f 0 ,f 2 ,f - 2 ,f 3 ,f 2ef ( 3 t ) f x = 3 x 2 - 2 f x = 1 x ,x3 2 x ,x ≤ 3
Determineasfórmulas paraf + g ,f - g , f g e f / g e obtenha os domínios das funções.27) f x = 2 x - 1 , g x = x - 1
Determineasfórmulas paraf + g ,f - g , f g e f / g e obtenha os domínios das funções.27) f x = x 1 + x 2 , g x = 1 x
Use o gráfico da renda media do exercício 5 para responder as seguintes questões, fazendo aproximações razoáveis quando for necessário.Qual foi o crescimento anuak médio da renda media entre 1993 e 19
Conforme mostra a figura abaixo, um pendulo de comprimento constante L faz um ângulo θ com a sua posição vertical. Expresse a altura h como uma função do ângulo θ .