Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.2 - Ex. 1
Um fabricante de latas sem tampas deseja usar folhas-de-flandres com dimensões de cm por cm, cortando quadrados iguais dos quatro cantos e dobrando os lados para cima. Use o método dessa seção para encontrar o comprimento do lado do quadrado a ser cortado, a fim de obter de cada folha-de-flandres uma caixa aberta, tendo o maior volume possível.
Passo 1
Essas questões têm um jeito bem metódico de resolver, saca só:
- Precisamos de uma equação que associe a variável que queremos maximizar e outra variável do problema. Essa é normalmente a parte mais difícil.
- Depois que temos essa função, vamos encontrar a derivada dela e procurar os valores onde ela se iguala a e os valores onde ela não existe.
- A partir do Teorema do Valor Extremo vamos encontrar os máximos e mínimos comparando os valores da função original nos extremos do intervalo e nos pontos onde a derivada é nula ou inexistente.
Passo 2
O problema diz que vamos tirar quadrados iguais dos lados e dobrá-los para cima. Vamos chamar o lado do quadrado de (em centímetros). Se um dos lados tem cm e o outro tem cm, quando cortarmos os quadrados de ambos os lados de cada um, ficaremos com de um lado e do outro. Isso porque foi tirado um quadrado de cada lado! Desse desenho:
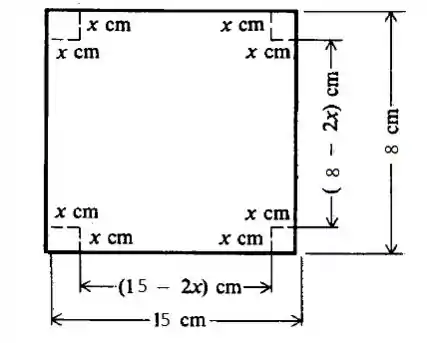
Figura fora de escala.
E o problema também diz que esses quadrados cortados de lado serão erguidos e farão a altura da caixa. Então o volume da caixa será o produto de cada uma dessas dimensões:
Simplificando:
Essa é a equação que procurávamos!
Passo 3
Agora precisamos determinar o intervalo fechado que estamos analisando. Repare que , pois não faria sentido falar de dimensões negativas. E pelo mesmo motivo: . E daí temos que Então o nosso intervalo fechado fica .
Agora derivando a função:
Como a derivada está definida para qualquer , vamos encontrar os pontos onde ela se anula:
Vamos facilitar a nossa vida e dividir tudo por :
Agora por bhaskara:
Daí temos as duas raízes:
E
Mas lembre-se do nosso intervalo: . Então podemos desconsiderar .
Passo 4
Agora vamos calcular a função original em cada ponto um dos três pontos (os extremos do intervalo e no valor de que acabamos de encontar). O valor de que tiver a maior imagem será o máximo da função no intervalo fechado!
Daí temos a nossa resposta!
Resposta
centímetros.