Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.6 - Ex. 50
Faça uma conjectura sobre o limite traçando o gráfico da função envolvida com um recurso computacional; verifique sua conjuctura usando a regra de L’Hôpital.
Passo 1
Quando montamos o gráfico dessa função computacionalmente, podemos observar que quando temos se aproximando pelo lado positivo, temos , no entanto, quando x se aproxima por a função não existe. Vamos ver se é isso mesmo calculando o limite...
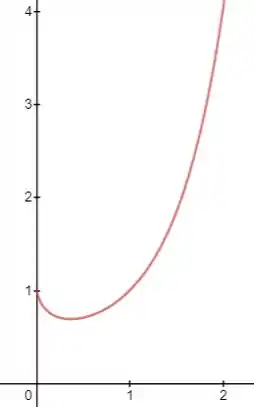
Passo 2
Para podermos aplicar a regra de l’hopital, temos que fazer umas manipulações aqui antes. Me acompanha:
Agora sim podemos aplicar o l’hopital.
Opa, então confirmamos que nosso limite realmente vai para 1!
Resposta
Exercícios de Livros Relacionados
Determinar os seguintes limites com auxílio das regras de L’Hospital. lim x → 2 1 2 x - 4 - 1 x - 2
Determinar os seguintes limites com auxílio das regras de L’Hospital. lim x → π 2 x c o t g x - π 2 cos x
Determinar os seguintes limites com auxílio das regras de L’Hospital. lim x → 1 1 2 1 - x - 1 3 1 - x 3
Determinar os seguintes limites com auxilio das regras de L’Hospital. lim x → 1 x 1 1 - x
Determinar os seguintes limites com auxilio das regras de L’Hospital. lim x → 3 1 x - 3 - 5 x 2 - x - 6