Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 22
Faça uma conjectura sobre o valor do limite (se ele existir) por meio dos valores da função nos números dados (com precisão de seis casas decimais).
Passo 1
Bora entender o que a gente vai fazer aqui!! O problema dá pra a gente esse limite:
E basicamente o que a gente quer é estimar quanto vale essa função quando ela se aproxima de zero.
O problema é que não podemos substituir o zero porque teríamos uma indeterminação (pois não existe)!
Então o que que o enunciado propõe pra a gente?!
A gente vai substituir o por vários valores que se aproximam cada vez mais do zero.
Bora lá!! 😉
Passo 2
Temos:
Os valores que a gente vai substituir são:
Construindo uma tabela com os valores de dados e os respectivos ficamos com:
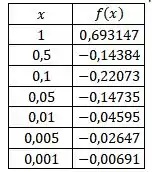
Perceba que quanto mais a gente vai aproximando o valor de para , também tende a se aproximar de zero.
Em outras palavras, podemos concluir que:
Entendeu direitinho?? Responde aee 😉