Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 20
Faça uma conjectura sobre o valor do limite (se ele existir) por meio dos valores da função nos números dados (com precisão de seis casas decimais).
Passo 1
Fala aí! Tudo beleza? Nessa questão várias substituições na função do limite que nos foi dada:
Nesse caso, vamos chamar
Com isso, vamos substituir os valores de que foram dados na função:
Nesse exercício a gente vai verificar o que acontece com quando se aproxima por valores à direita e à esquerda de .
Em outras palavras, estamos trabalhando com os limites laterais!!
Ah, lembre-se que um limite só existe em um ponto se seus limites laterais forem iguais!!
Bora lá!! 😉
Passo 2
Vamos construir duas tabelas relacionando com .
A tabela abaixo mostram os valores de que se aproximam de pela direita, ou seja, :
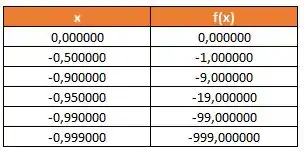
Já esta tabela mostram os valores de que se aproximam de pela esquerda, ou seja :
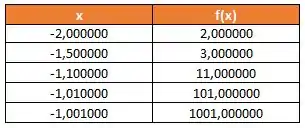
Pela análise da tabela, podemos concluir que o limite não existe, pois quando temos que e quando temos que .
Entendeu direitinho?? Responde aee 😉
Resposta
O limite não existe, pois quando temos que e quando temos que