Represente geometricamente o campo vetorial dado.
c)
(observe:
Passo 1
Veja que . Ou seja, a intensidade do campo vetorial é a mesma em todos os pontos da circunferência de centro na origem. Nesse caso a intensidade em cada ponto é igual ao raio da circunferência de centro na origem que passa por esse ponto.
A gente ainda tem que , o que quer dizer que o campo vetorial é sempre tangente a essas circunferências.
O desenho do campo é esse:
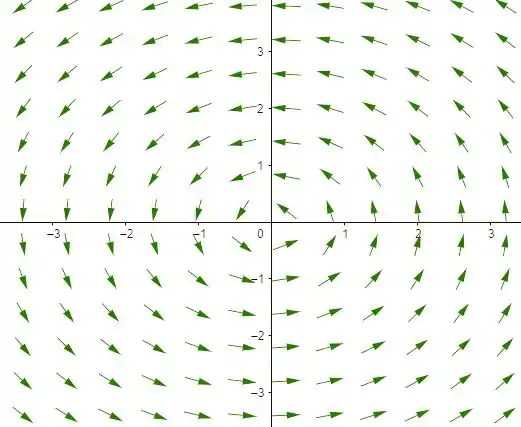
Resposta
Ei, a resposta está no passo a passo :)