Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.2 - Ex. 1b
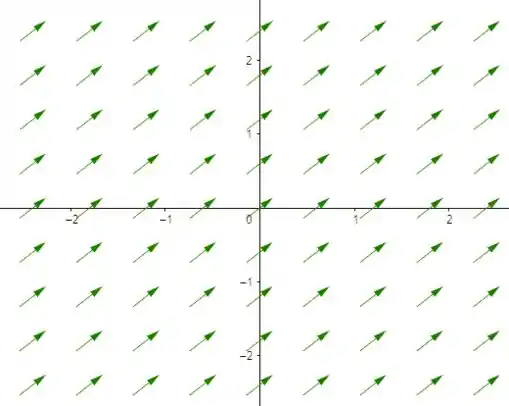
Represente geometricamente o campo vetorial dado.
b)
Passo 1
Vamos começar calculando a intensidade do campo. Para isso a gente faz a norma:
Ou seja, a cada ponto do plano, o campo associa um vetor de intensidade e da forma .
Temos a representação geométrica do campo assim:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
7. Determine uma função potencial para cada campo gradiente F dado b. F x , y = 2 x y 2 - y 3 ,2 x 2 y - 3 x y 2 + 2
7. Determine uma função potencial para cada campo gradiente F dado a. F x , y = e x sen y ,e x cos y
6. Calcule o trabalho realizado pelo campo de força F x , y , z = y 2 ,z 2 , x ² ² Ao longo da curva obtida como interseção da esfera x 2 + y 2 + z 2 = a 2 Com o cilindro x 2 + y 2 = a x Onde z ≥ 0,a
7. Determine uma função potencial para cada campo gradiente F dado e. F x , y , z = e y + 2 z ,x e y + 2 z ,2 x e y + 2 z
7. Determine uma função potencial para cada campo gradiente F dado c. F x , y = 3 x 2 + 2 y - y 2 e x ,2 x - 2 y e x