Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 14

Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante.

r u , v = u v 2 i + u 2 v j + ( u 2 - v 2 ) k

Passo 1

Iai galera , o exercício nos pede para que encontremos o gráfico que corresponderá a equação:

r u , v = u v 2 i + u 2 v j + ( u 2 - v 2 ) k

E depois determinar quais famílias de curva da grade terão u constante e quais terão v constante.

Então , a primeira coisa que precisamos fazer é achar os valores que correspondem a x , y   e   z . A gente faz isso para conseguir visualizar melhor o comportamento da superfície.

O próximo passo é avaliar como a ficam as nossas equações quando u constante e quando v constante.

Juntando essas informações seremos capazes de achar o gráfico correspondente.

Passo 2

Então vamos começar identificando quem são x , y   e   z . Sabemos que a nossa equação é:

r u , v = u v 2 i + u 2 v j + ( u 2 - v 2 ) k

Logo:

x = u v 2

y = u 2 v

z = ( u 2 - v 2 )

Passo 3

Agora o próximo passo é avaliar quando v   e   u   serão constantes.

vamos começar por u :

x = ( c t e ) . v 2

y = ( c t e ) 2 v

z = c t e 2 - v 2

Se isolarmos o v , teremos que :

v = y c t e 2

v = 1 c t e x

Substituindo nas equações :

→ x = ( c t e ) . v 2

x = c t e y c t e 2 2 = 1 c t e 3 y 2

→ z = c t e 2 - v 2

z = c t e 2 - 1 c t e x

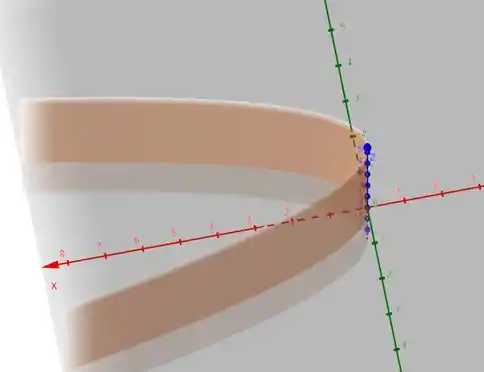
Nesse caso, cada curva de grade correspondente a u está no plano z = c t e 2 - 1 c t e x e sua projeção no plano x y é uma parábola x = k y 2 . Vamos ver graficamente para ficar mais fácil de visualizar.

Passo 4

Agora vamos fazer v constante :

x = u ( c t e ) 2

y = u 2 ( c t e )

z = ( u 2 - ( c t e ) 2 )

Vamos isolar o u :

u 2 = y c t e

u = 1 c t e 2 x

Substituindo nas equações:

→ y = u 2 ( c t e )

                        y = x c t e 2 c t e = 1 c t e 3 x 2

→ z = u 2 - c t e 2

z = 1 c t e y - c t e 2

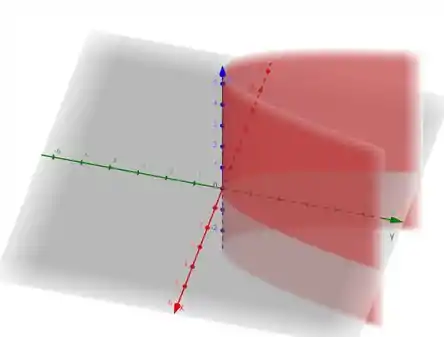
Cada linha da curva de grade no plano z = 1 C t e y - c t e 2 e sua projeção no plano x y é uma parábola y = k x 2 .

Passo 5

Juntando os dados que encontramos anteriormente podemos dizer que o gráfico que mais se assemelha a isso é o 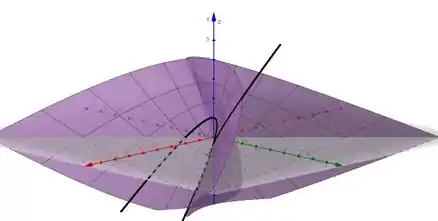V I !

Resposta

Gráfico V I .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine uma representação paramétrica para a superfície.A parte da esfera x 2 + y 2 + z 2 = 16 que está entre os planos z = - 2 e z = 2
Determine as equações paramétricas da superfície obtida pela rotação da curva x = 4 y 2 - y 4 , - 2 ≤ y ≤ 2 em torno do eixo y e use-as para traçar o gráfico da superfície.
Determine uma representação paramétrica para a superfície.A parte do plano z = x + 3 que está dentro do cilindro x 2 + y 2 = 1
O que acontecerá com o tubo espiral do Exemplo 2 (veja a Figura 5 ) se substituirmos cos ⁡ u por sen ⁡ u e sen ⁡ u por cos ⁡ u ?O que acontecerá se substituirmos cos ⁡ u por cos ⁡ 2 u e sen ⁡ u por se
Determine as equações paramétricas da superfície obtida pela rotação da curva y = e - x , 0 ≤ x ≤ 3 , em torno do eixo x e use-as para traçar o gráfico da superfície.