Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 19
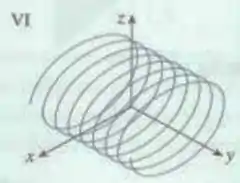
Faça uma correspondência entre as equações paramétricas e os gráficos (identificados com números de ). Justifique sua escolha.
Passo 1
Fala ai galera! Tranquilo?
Para comelarmos esta questão vamos verificar qual curva é formada pelas equações paramétricas dadas no enunciado. Precisamos observar individualmente cada uma das coordenadas e como elas variam com o parâmetro .
Vamos começar!
Passo 2
Esta função descreve a coordenada da curva. O cosseno varia entre e enquanto varia. Isso sugere que oscila entre e enquanto 𝑡t varia. Portanto, a coordenada da curva descreve uma oscilação no intervalo .
Esta função descreve a coordenada da curva. Ela varia linearmente com , o que significa que aumenta ou diminui uniformemente à medida que aumenta ou diminui. Portanto, a coordenada da curva descreve uma reta inclinada com um ângulo de graus em relação ao eixo .
Esta função descreve a coordenada da curva. O seno varia entre e enquanto varia, então oscila entre e . Portanto, a coordenada da curva descreve uma oscilação no intervalo .
Passo 3
Ao combinar essas coordenadas, a curva formada é uma hélice que se estende ao longo do eixo , enquanto oscila em altura e distância do eixo . Isso significa que é uma hélice tridimensional.
Saca só! A oscilação de e sugere que a curva se estende em torno do eixo e varia em altura e distância do eixo .
A variação linear de sugere que a curva se estende ao longo do eixo , formando uma linha reta.
Podemos então interpretar as equações sendo representados pela curva de número .
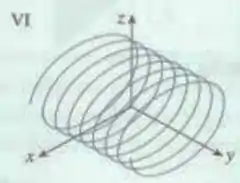
Resposta
