Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 21
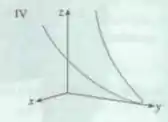
Faça uma correspondência entre as equações paramétricas e os gráficos (identificados com números de ). Justifique sua escolha.
Passo 1
Fala ai galera! Tranquilo? Aqui temos as equações paramétricas:
E os seguintes gráficos:
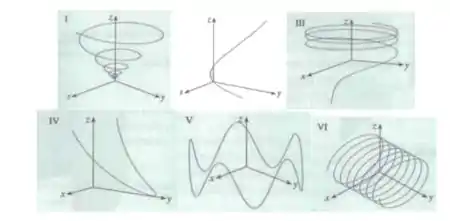
Para começarmos esta questão vamos verificar qual curva é formada pelas equações paramétricas dadas no enunciado. Precisamos observar individualmente cada uma das coordenadas e como elas variam com o parâmetro para conseguirmos associa-las ao gráfico.
Vamos começar!
Passo 2
Descreve uma função linear em relação a , onde a coordenada cresce uniformemente com .
Descreve uma função que varia conforme aumenta, onde diminui à medida que aumenta, mas nunca atinge zero.
Descreve uma função quadrática em relação a , onde a coordenada aumenta de forma quadrática com .
Passo 3
A equação está associada aos gráficos , , e , pois descreve um crescimento linear de com .
A equação está associada aos gráficos , , e , pois descreve uma diminuição de com e nunca atinge zero.
A equação está associada aos gráficos e , pois descreve um crescimento quadrático de com .
Passo 4
Que tal fazermos uma conclusão de toda essa análise? A curva formada pelas equações paramétricas é uma curva tridimensional que se estende infinitamente em direção positiva nos eixos e , enquanto a coordenada diminui conforme aumenta, mas nunca atinge zero.
Essa curva tem características de uma superfície em forma de cunha, abrindo-se conforme se move para longe do plano .
Podemos então interpretar as equações sendo representados pela curva de número .
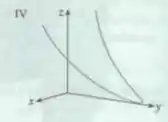
Resposta
Gráfico
