Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.1 - Ex. 11
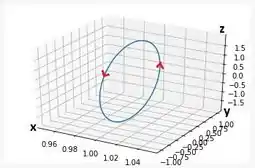
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro tcresce.
Passo 1
Fala ai pessoal! Tranquilo?
Vamos entender um pouco sobre essa questão?
A equação é uma equação vetorial, logo ele é composto pelas componentes que correspondem respectivamente aos eixos . Para conseguirmos esboçar o gráfico temos que estipular valores de para termos pontos da curva.
Vamos começar?
Passo 2
Substituindo so valor de
Para , as coordenadas são
Para , as coordenadas são
Para 𝑡=𝜋t=π, as coordenadas são
Passo 3
Será melhor construirmos uma tabela para vermos os pontos e termos uma noção da curva formada.
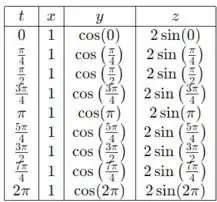
Passo 4
Vamos agora rerificar o valor do raio através de uma relação trigonométrica para o valor de e .
Vamos eliminar esse do lado do seno para poder fazer a nossa identidade trigonométrica
E isso, meus caros, é a famosa equação da elipse, então no final das contas temos uma elipse no plano e raio igual a .
Passo 5
E por fim, toda essa analise nos seu a seguinte curva:
A curva descrita pela equação vetorial é um círculo de raio no plano , centrado em , visto que é constante e igual a . A direção na qual o parâmetro cresce é indicada no sentido anti-horário quando visto de cima para baixo.
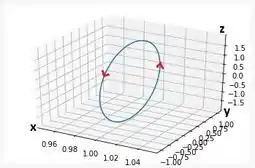
O parâmetro está crescento ao longo do plano no sentido anti-horário, como indicado pelas setas ao longo da elipse.
Resposta
