Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 4
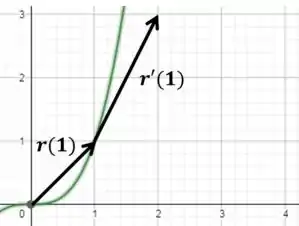
(a) Esboce o gráfico da curva plana com a equação vetorial dada.
(b) Encontre
(c) Esboce o vetor posição e o vetor tangente para o valor dado de .
Passo 1
Eaee, belezinha?? Bom... nos foi dada a seguinte equação vetorial:
Na letra (a) queremos esboçar o gráfico dessa curva. Para isso, basta pegarmos as equações paramétricas, isolar o parâmetro de uma e inserir na outra de forma que fique uma função do tipo .
Em seguida, na letra (b), devemos determinar a derivada . Para isso, basta derivarmos as equações paramétricas individualmente em relação a .
Por fim, na letra (c), iremos esboçar o vetor posição e o vetor tangente para .
Agora bora lá!! 😉
Passo 2
As equações paramétricas correspondentes à função vetorial dada são:
Isolando-se na primeira equação obtemos . Substituindo esse resultado na segunda equação temos:
Com isso, plotando o gráfico, teremos:
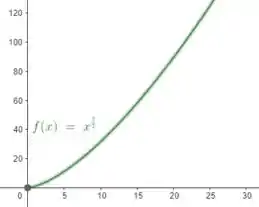
O nosso gráfico foi construído utilizando o GeoGebra, para melhor visualização sua.
Passo 3
Determinamos derivando as componentes de :
Passo 4
O vetor posição em é:
Por outro lado, o vetor tangente em , tem origem no ponto e é dado por:
Dessa forma podemos representar os vetores:
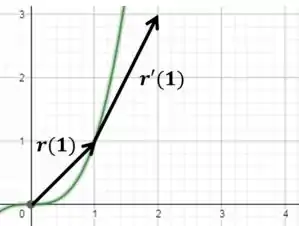
Então veja que o vetor:
Temos então que:
E
E vemos isso no gráfico.
Para o pensamento é o mesmo, porém estamos começando o vetor no ponto de tangencia .
Resposta
(a)
(b)
(c)
