Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.1 - Ex. 22

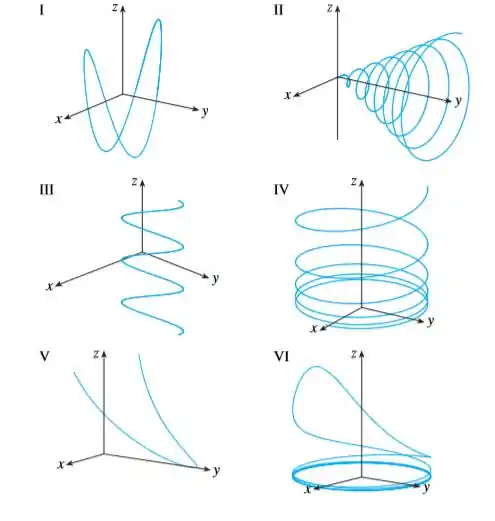
Faça uma correspondência entre as equações paramétricas e os gráficos (identificados com números de I-VI). Justifique sua escolha.

x = cos ⁡ t   ,     y = s e n t ,     z = 1 1 + t 2

Passo 1

Oie, meu amigo. Vou te ajudar a resolver essa atividade hoje.

Basicamente aqui a gente tem que encontrar qual gráfico representa a curva parametrizada:

x = cos ⁡ t       y = s e n t     z = 1 1 + t 2

Para esse caso, a gente pode utilizar a identidade trigonométrica:

sin 2 ⁡ x + cos 2 ⁡ x = 1

Para nos ajudar a entender o comportamento da função.

Passo 2

Em todo ponto sobre a curva dada nós temos no eixo x y :

x 2 + y 2 = cos 2 ⁡ t + s e n 2 t

E por conta da identidade trigonométrica, teremos que:

x 2 + y 2 = 1

Dessa forma, a curva está em um cilindro circular x 2 + y 2 = 1 com eixo no eixo z .

Note que:

z = 1 1 + t 2

Então o denominador tem a seguinte limitação:

1 + t 2 ≥ 1

dessa forma 0 < z ≤ 1 , ou seja, ela é limitada. O gráfico deve ser o V I .

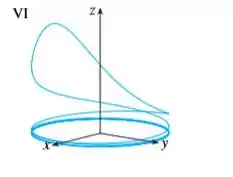
Resposta

O gráfico deve ser o V I .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a função vetorial que representa a curva obtida pela intersecção das duas superfícies. O cone z = x 2 + y 2 e o plano z = 1 + y .
Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q p - 2,4 , 0 , Q ( 6 , - 1,2 )
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t = cos ⁡ ti - cos ⁡ t j + sin ⁡ t k
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t =1 + t , 3 t ,- t
Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. x = e - tcos ⁡ t y = e - t sin ⁡ tz = e - t ( 1,0 , 1 )